One question: How do they describe the problem to the AI? AI has to understand the problem just like human participants or the problem is specified in some formal language?Amber G. wrote:I don't know all the results.. will be interesting to see how AI did in this IMO...
BR Maths Corner-1
Re: BR Maths Corner-1
Re: BR Maths Corner-1
From what I have seen - AI at present - best programs quite routinely - can fairly easily understand the problems as written. At present exceptVayutuvan wrote:One question: How do they describe the problem to the AI? AI has to understand the problem just like human participants or the problem is specified in some formal language?Amber G. wrote:I don't know all the results.. will be interesting to see how AI did in this IMO...
for IMO level problems, many other contest (even JEE type problems, from what I have seen) problems are no challenge to best AI programs. (They can crack JEE math type questions
Heck even brf problems given by me - at least for most parts I tried
For example we spent a few pages here for x^2 - 61y^2 = 1, I just typed "solve in integers x^2-61y^2=1 and I got the complete result.
Re: BR Maths Corner-1
Will be nice to see interesting discussion it generates.sudarshan wrote:
I suspected that was the case, let me see if I can get there. That insight about "if the numbers are all even, then divide them by 2" is a good one, of course it only works because of that "x1 + 4*y" property, else it would yield mixes of odd/ even again.
My solution, which I thought earlier, was a little too complicated and some solution I have seen are also long.. but I have found a method which is very nice.. will put when I get some time.
Reducing all even numbers (so that only case you have to consider are all odd numbers) can be thought in a much simpler way. If the set contains all the even numbers say 2a , 2b, 2c, 2d, 2e, 2f, 2g ....and it works then the set (a,b,c,d,e,f,g) will work too. (for example if AM of 2a and 2b is GM of (2c, 2d and 2e) then AM of a and b will be GM of (c,d,e).
So one can consider only odd numbers without loss of generality.
Re: BR Maths Corner-1
Just thinking out loud.
Let's say that we have n odd numbers with the property, that the AM of any pair, can be represented as the GM of a set of 1 or more numbers from the same set. If all n numbers are the same number, we have no problem. We want to see if we can find a set of n numbers, where all numbers are not the same value, which will satisfy the condition. So in such a set, by definition, one number will be the largest, and one number will be the second largest (there could be multiple instances of the largest and/ or second largest number in the set, of course).
Let's say the largest value in the set is y, and the second largest value is x. If there are other unique numbers in the set, then they are all smaller than x.
1. There is no number in the set larger than y.
2. There is also no number in the set, which lies between x and y (since x is the second largest number).
3. The arithmetic mean of x and y is a = (x+y)/2.
3.a. Since x < y, that means x < a < y (i.e., x is strictly less than a, and a is strictly less than y, meaning, a lies between x and y).
3.b. Since x is at least 1, y cannot be a multiple of a (1*a < y, and 2*a = x+y, which is already larger than y).
4. There has to be some combination of one or more numbers in the set, whose GM equals a = (x+y)/2.
4.a. The GM of any k numbers g1, g2, ... gk is (g1*g2*...gk)^(1/k).
5. If the set <g1, g2, ... gk> (which is a subset of the full set of n numbers) consists of just one number g1 - then by definition, its GM is g1 itself. So by 4., g1 will have to be the same as a, which lies between x and y. But g1 is a member of the full set of n numbers, and by 2., there is no number in the set between x and y.
So there have to be at least two numbers in the set, such that their GM equals the value a = (x+y)/2.
But x is the second largest value in the set, and y is the largest. If the two numbers are y and y (assuming multiple occurrences of y in the set), the GM will be y itself, which is too large (3.a). If the two numbers are x and x (assuming multiple occurrences of x in the set), the GM will be x itself, which is too small (3.a).
How about x and y? Recall, the AM of two unequal positive numbers will *always* be larger than its GM. So even x and y won't work. And the other numbers in the set of n are smaller than x (x is the second largest, remember?) so they definitely won't work.
6. We need a way to "pull up" the value of the GM to be a = (x+y)/2. So we need to include more numbers in the GM calculation, which are large enough to pull the GM up. x, however, is already smaller than a, and will pull *down* the GM value. So these additional numbers can only be further occurrences of y (since y is the only number in the set of n, which is larger than a). Thus, it is necessary to have multiple occurrences of the largest number, y in the set.
Of course, if we include many instances of y in the GM set, we can include a few x's (or even numbers smaller than x) since the many instances of y will compensate for these smaller numbers.
If the GM calculation set <g1, g2, ... gk> has "k" numbers, then, a^k has to be the product of all the numbers in the GM calculation set. This means the numbers in the GM calculation set can only be composed of the factors of a, and can have no other factors. From 3.b., y is also not a multiple of a.
So y is a number larger than a, all of whose factors are also factors of a, and the set <g1, g2, ... gk> also has multiple occurrences of y in it (i.e., many of the values of g1, g2, ... are actually y itself). <g1, g2, ... gk> also consists of at least 3 numbers, of which at least two are equal to y (see 6.).
Still thinking from here on....
Let's say that we have n odd numbers with the property, that the AM of any pair, can be represented as the GM of a set of 1 or more numbers from the same set. If all n numbers are the same number, we have no problem. We want to see if we can find a set of n numbers, where all numbers are not the same value, which will satisfy the condition. So in such a set, by definition, one number will be the largest, and one number will be the second largest (there could be multiple instances of the largest and/ or second largest number in the set, of course).
Let's say the largest value in the set is y, and the second largest value is x. If there are other unique numbers in the set, then they are all smaller than x.
1. There is no number in the set larger than y.
2. There is also no number in the set, which lies between x and y (since x is the second largest number).
3. The arithmetic mean of x and y is a = (x+y)/2.
3.a. Since x < y, that means x < a < y (i.e., x is strictly less than a, and a is strictly less than y, meaning, a lies between x and y).
3.b. Since x is at least 1, y cannot be a multiple of a (1*a < y, and 2*a = x+y, which is already larger than y).
4. There has to be some combination of one or more numbers in the set, whose GM equals a = (x+y)/2.
4.a. The GM of any k numbers g1, g2, ... gk is (g1*g2*...gk)^(1/k).
5. If the set <g1, g2, ... gk> (which is a subset of the full set of n numbers) consists of just one number g1 - then by definition, its GM is g1 itself. So by 4., g1 will have to be the same as a, which lies between x and y. But g1 is a member of the full set of n numbers, and by 2., there is no number in the set between x and y.
So there have to be at least two numbers in the set, such that their GM equals the value a = (x+y)/2.
But x is the second largest value in the set, and y is the largest. If the two numbers are y and y (assuming multiple occurrences of y in the set), the GM will be y itself, which is too large (3.a). If the two numbers are x and x (assuming multiple occurrences of x in the set), the GM will be x itself, which is too small (3.a).
How about x and y? Recall, the AM of two unequal positive numbers will *always* be larger than its GM. So even x and y won't work. And the other numbers in the set of n are smaller than x (x is the second largest, remember?) so they definitely won't work.
6. We need a way to "pull up" the value of the GM to be a = (x+y)/2. So we need to include more numbers in the GM calculation, which are large enough to pull the GM up. x, however, is already smaller than a, and will pull *down* the GM value. So these additional numbers can only be further occurrences of y (since y is the only number in the set of n, which is larger than a). Thus, it is necessary to have multiple occurrences of the largest number, y in the set.
Of course, if we include many instances of y in the GM set, we can include a few x's (or even numbers smaller than x) since the many instances of y will compensate for these smaller numbers.
If the GM calculation set <g1, g2, ... gk> has "k" numbers, then, a^k has to be the product of all the numbers in the GM calculation set. This means the numbers in the GM calculation set can only be composed of the factors of a, and can have no other factors. From 3.b., y is also not a multiple of a.
So y is a number larger than a, all of whose factors are also factors of a, and the set <g1, g2, ... gk> also has multiple occurrences of y in it (i.e., many of the values of g1, g2, ... are actually y itself). <g1, g2, ... gk> also consists of at least 3 numbers, of which at least two are equal to y (see 6.).
Still thinking from here on....
Re: BR Maths Corner-1
^^^ Very good. Agree with point 1 to 6.
Big Hint: Going along the line, I can think of *simpler* point 7 (and possibly 8 ) which finishes your proof.
(Even bigger hint: read *carefully* my previous post (just above yours) .
.
Leave it at that, to see someone else or you write down the final argument.
(The problem was posed by an Estonian professor - I liked the problem)
Big Hint: Going along the line, I can think of *simpler* point 7 (and possibly 8 ) which finishes your proof.
(Even bigger hint: read *carefully* my previous post (just above yours)
Leave it at that, to see someone else or you write down the final argument.
(The problem was posed by an Estonian professor - I liked the problem)
Re: BR Maths Corner-1
^^ I like the problem because, at first site it looks like a combinatorial problem with algebra but it is a little deeper than that.
For example if the statement was changed from positive integers to rational numbers, it will still work, but if you allow all numbers, it does not. (except for the case of only 2 numbers).
One can have, ( (√5 -2), 1, 1) where GM of all three numbers is indeed AM of first two. But in *all* such cases, at least one number has to come out irrational.
For example if the statement was changed from positive integers to rational numbers, it will still work, but if you allow all numbers, it does not. (except for the case of only 2 numbers).
One can have, ( (√5 -2), 1, 1) where GM of all three numbers is indeed AM of first two. But in *all* such cases, at least one number has to come out irrational.
Re: BR Maths Corner-1
Okay here is just a pure algebra problem, simple looking, from the same contest - posting here because it is so similar to all the thinking above.
Given a ≥ b ≥ c≥ d>0 and a+b+c+d=1.
prove:
(a+2b+3c+4d) (a^a b^b c^c d^d ) < 1.
Given a ≥ b ≥ c≥ d>0 and a+b+c+d=1.
prove:
(a+2b+3c+4d) (a^a b^b c^c d^d ) < 1.
Re: BR Maths Corner-1
Let us modify the problem a little.SriKumar wrote:vayutuvan- thanks for the link but right now I am still trying to wrap my mind around how the square root (!) of the product of two irrational numbers (!!) e & pi, can be exactly equal to anything
Instead of "Prove that" <equality>, make it "Prove or disprove" or "It is conjectured that" and replace the <equality> with the language of real analysis.
What will you do first? You will start by evaluating both RHS and LHS in double precision, double double precision, and so on. You might stop at some reasonable error say like 1.0e-16 (which is considered to be "numerical zero" in 64 bit double computations) or may be even go down 1.0e-312 (which is close to the "numerical zero" in quad precision).
If that works out, then you start looking to prove it using real analysis methods, i.e. convergence of the sequence given in the LHS to a sequence that represents the RHS. Much harder. @Amber G. said "Prove that" which lets you skip the step of experimentation with large numbers and high precision arithmetic.
Re: BR Maths Corner-1
FWIW: Some tidbits of this Olympiad.
Rank - China (1), Russia (2), USA (3) India did not take part.
The problem I posted - All USA kids scored 100% ..
(Was curious so looked up score for Pakistan - 0 people solved the problem)
Rank - China (1), Russia (2), USA (3) India did not take part.
The problem I posted - All USA kids scored 100% ..
(Was curious so looked up score for Pakistan - 0 people solved the problem)
Re: BR Maths Corner-1
Not able to finish that solution, a simple end is still eluding me. I got another couple of steps further, but it's getting more complex all the time.
VT, I verified (numerically) that the series on the RHS plus that continued fraction does come to the LHS on that e/ pi problem. Now what? Expand the series for e and pi, multiply terms, mix and match?
VT, I verified (numerically) that the series on the RHS plus that continued fraction does come to the LHS on that e/ pi problem. Now what? Expand the series for e and pi, multiply terms, mix and match?
Re: BR Maths Corner-1
Here it is:sudarshan wrote:Not able to finish that solution, a simple end is still eluding me. I got another couple of steps further, but it's getting more complex all the time.
Assuming we have already agreed that we have to only to consider the case when all the numbers are odd.
(If all numbers are even - or divisible by any one number for that matter - can be factored out. This was a big hint).
We already proved the case for two so let us assume the total number in the set is >2
- Let L be the largest number in the set.
- It has to be an odd number greater than 1 (else all numbers will be equal
- let p an odd prime ( greater than or equal to 3) divides L
- Let L2 be the next largest number (which is equal or less than L).
Now if L2 is not divisible by p
Then AM (= (L+L2)/2) of L and L2 is also not divisible by p
In this case (since L2 and L are obviously not equal - as L2 is not divisible by P) the AM is greater than L2.
But it is GM of some numbers - out of which L can not be there as one of the numbers . (otherwise p will divide this GM).
But GM of numbers (where *every* possible number remaining is equal or Less than L2) can not be greater than L2.
This is impossible . Contradiction!
==> L2 must be divisible by p.
Now same logic for L3- the next largest number.
AM of L and L3 will be larger than L3, and since L2 and L can not be included (as both are divisible by p).
L3 must also be divisible by p (remember p is an odd prime)
Rinse and repeat!
Next largest number must also be divisible by p .. and so it the next largest number ...
So all numbers must be divisible by p !!
Rest is simple - Fermat's infinite descend - Divide all numbers by p and repeat the process on this new set of numbers !!!!
Only way it can end is when the largest number now becomes 1 but in that case all the numbers now have to be equal to 1.)
QED!
(My first solution which I thought was quite a bit more complex but I like the above as it is fairly easy to understand and does not use complicated math)
Re: BR Maths Corner-1
This is what I was missing! I got that L and L2 should both be divisible by a prime factor of the AM, but I arrived at it in a different way, and missed the first statement above..
.
.
1. But it is GM of some numbers - out of which L can not be there as one of the numbers . (otherwise p will divide this GM).
.
.
.
2. Now same logic for L3- the next largest number.
...
For the second statement, I figured that all the lower numbers had to be divisible by the same prime factor, but didn't think of repeating the logic with the next largest number. So I wasn't able to prove that intuition.
So close!
Re: BR Maths Corner-1
^^^ Yes...
(The critical part was to see that every prime factor of L must also be a factor of L2 (and thus all other numbers)..The problem becomes a number-theory problem rather than combinatorial which was a interesting part)
(The critical part was to see that every prime factor of L must also be a factor of L2 (and thus all other numbers)..The problem becomes a number-theory problem rather than combinatorial which was a interesting part)
Re: BR Maths Corner-1
I saw this. I will answer after collecting my thoughts.sudarshan wrote:VT, I verified (numerically) that the series on the RHS plus that continued fraction does come to the LHS on that e/ pi problem. Now what? Expand the series for e and pi, multiply terms, mix and match?
Re: BR Maths Corner-1
^^^ Trouble or interesting part is there are many examples in math which sometimes boggle even humans. For me, for example one the following from Ramanujan's time --
If Pi(x) is number of primes less than x and Li(x) = integral of 1/log (t) from 0 to x.
Then Pi(x) - Li(x) > 0 is true for x =1, 2, 3, .... 1000, 1000,000 .....10000000000000, ...
It is true for 1 billion .. 1 billion billion .. i billion billion billion but not NOT for all numbers ..
You have to go about 10^300 or more to find that the number becomes -ive
If Pi(x) is number of primes less than x and Li(x) = integral of 1/log (t) from 0 to x.
Then Pi(x) - Li(x) > 0 is true for x =1, 2, 3, .... 1000, 1000,000 .....10000000000000, ...
It is true for 1 billion .. 1 billion billion .. i billion billion billion but not NOT for all numbers ..
You have to go about 10^300 or more to find that the number becomes -ive
Re: BR Maths Corner-1
For those who are interested in Ramanujan's work here is a current talk - from none other than Prof Ono ( Kyoto RIMS) in case you want to watch - the link will work for next 7 days..
quantum modular forms and representation theory
(In my humble opinion - this talk is excellent - happens to deal with some of the points/theory behind some of the topics we were talking about (eg elliptical functions/cubic equations) - it is understandable too for people like me as it puts many complex items in simpler terms)
quantum modular forms and representation theory
(In my humble opinion - this talk is excellent - happens to deal with some of the points/theory behind some of the topics we were talking about (eg elliptical functions/cubic equations) - it is understandable too for people like me as it puts many complex items in simpler terms)
Re: BR Maths Corner-1
Thursday (In Hindi = गुरुवार - A day to honor Gurus).
Pictured here are two gurus - great mathematicians - who were also great human beings. One of them received Nobel Prize and the other was honored by "Bharat Ratn "- (the highest civilian award given by India).

Can you identify them?
Here they are getting the honors:

Pictured here are two gurus - great mathematicians - who were also great human beings. One of them received Nobel Prize and the other was honored by "Bharat Ratn "- (the highest civilian award given by India).

Can you identify them?
Here they are getting the honors:

Re: BR Maths Corner-1
Ben Sparks explains (and codes) the so-called SIR Model being used to predict the spread of cornavirus (COVID-19).
More links (see in the youtube)
https://youtu.be/k6nLfCbAzgo
More links (see in the youtube)
https://youtu.be/k6nLfCbAzgo
Re: BR Maths Corner-1
Maharshi Karve.Amber G. wrote:Thursday (In Hindi = गुरुवार - A day to honor Gurus).
Pictured here are two gurus - great mathematicians - who were also great human beings. One of them received Nobel Prize and the other was honored by "Bharat Ratn "- (the highest civilian award given by India).
Can you identify them?
Here they are getting the honors:
Re: BR Maths Corner-1
^^^ Yes, left of Maharshi Prof Karve is Physicist Albert Einstein. Photo (if I am not mistaken) was taken in Germany.
Re: BR Maths Corner-1
Amber G ji, maybe you could suggest to Dr. Vidyasagar et al, that the bijaganita (tr.: algebraic; literally: "seed mathematics") terms in that supermodel could use Sanskrit aksharas instead of Greek letters. There's more than enough letters in Indian languages, and after all, the concept of bijaganita did originate in India.
Re: BR Maths Corner-1
Nice article about Ashwin Sah. A really a bright star.
Undergraduate Math Student Pushes Frontier of Graph Theory

( Few years ago, I mentioned Ashwin's name in this dhaga - he won a IMO gold medal at a very young age. He is at MIT. He was a REU student of prof Ken Ono - mentioned several times here in this dhaga - In a few years potential for another Fields Medal. )
Undergraduate Math Student Pushes Frontier of Graph Theory

( Few years ago, I mentioned Ashwin's name in this dhaga - he won a IMO gold medal at a very young age. He is at MIT. He was a REU student of prof Ken Ono - mentioned several times here in this dhaga - In a few years potential for another Fields Medal. )
Re: BR Maths Corner-1
AmberG ji, very talented - those two kids. (You probably know that but for others who are reading) Ramsey Theory is a generalization of the Pigeon Hole Principle (PHP). You talked about the PHP in this thread before.
That reminds me to post the following puzzle from Martin Gardiner's SA column. I apologize if it was posted before.
Given an n sided polyhedron, i.e. a polyhedron with n faces each face being a polygon, prove that there exist two faces which have an equal number of sides.
That reminds me to post the following puzzle from Martin Gardiner's SA column. I apologize if it was posted before.
Given an n sided polyhedron, i.e. a polyhedron with n faces each face being a polygon, prove that there exist two faces which have an equal number of sides.
Re: BR Maths Corner-1
I have not seen the problem before (I used to think that I have seen all such problems - at least those which has appeared in SA or such magazines or popular books or .. have been asked in popular contests ..Vayutuvan wrote:
That reminds me to post the following puzzle from Martin Gardiner's SA column. I apologize if it was posted before.
Given an n sided polyhedron, i.e. a polyhedron with n faces each face being a polygon, prove that there exist two faces which have an equal number of sides.
(Hint: It is not hard - If you apply Euler's formula)
Last edited by Amber G. on 02 Dec 2020 05:53, edited 1 time in total.
Re: BR Maths Corner-1
From American Mathematical Society's FB pageVayutuvan wrote:AmberG ji, very talented - those two kids. .
Ashwin Sah and Mehtaab Sawhney, both currently graduate mathematics students at MIT, will receive the 2021 AMS-MAA-SIAM Frank and Brennie Morgan Prize for Outstanding Research in Mathematics by an Undergraduate Student.

Re: BR Maths Corner-1
Mark your calendars - this may be of interest to many..

(Manjul Prakash is India's first Fields Medal winner, not only a brilliant mathematician but also an extremely good speaker)

(Manjul Prakash is India's first Fields Medal winner, not only a brilliant mathematician but also an extremely good speaker)
Re: BR Maths Corner-1
Dr. Carolina Araujo is only the second women mathematician to receive the Ramanujan Prize in its long history.
She is invited by Govt of India to give lectures and have interactions especially with budding and aspiring women mathematicians and later visit India.
It was interesting to see four Ambassadors joining the award function..
More at: https://dst.gov.in/2020-ramanujan-prize ... ina-araujo
She is invited by Govt of India to give lectures and have interactions especially with budding and aspiring women mathematicians and later visit India.
It was interesting to see four Ambassadors joining the award function..
More at: https://dst.gov.in/2020-ramanujan-prize ... ina-araujo
Re: BR Maths Corner-1
Two very interesting .. not to be missed lectures. Open to public.
Indian Academy of Sciences “National Mathematics Day” lectures.
Infinity and Beyond Series:
- December 21 st (6:30 PM IST) - Why does Ramanujan, 'the man who knew infinity' matters. (By prof Ken Ono)
- December 22 nd (4 PM IST) - Marvelous Number Pi (By Prof R Bhatia)
Indian Academy of Sciences “National Mathematics Day” lectures.
Infinity and Beyond Series:
- December 21 st (6:30 PM IST) - Why does Ramanujan, 'the man who knew infinity' matters. (By prof Ken Ono)
- December 22 nd (4 PM IST) - Marvelous Number Pi (By Prof R Bhatia)
Re: BR Maths Corner-1
^^^ Those lectures were extremely good and I recommend it - for general public. (Check out the link).
Today is Ramanujan's Birthday.
India is celebrating it as National Mathematics day.
So on this day, let me reproduce a result from Ramanujan - which he famously wrote in his first letter to Hardy:
He introduce a function (continued fraction, which I have talked about many times in this thread):
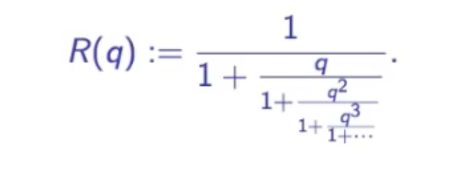
Now when q=1, solving it is not very hard...
(If answer is x then x = 1/(1+x) which gives the value of x
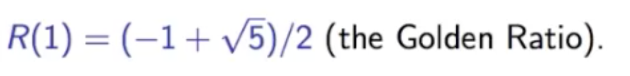
But can you find R(q) for other values of q.
(Hardy was completely stumped).
Today is Ramanujan's Birthday.
India is celebrating it as National Mathematics day.
So on this day, let me reproduce a result from Ramanujan - which he famously wrote in his first letter to Hardy:
He introduce a function (continued fraction, which I have talked about many times in this thread):

Now when q=1, solving it is not very hard...
(If answer is x then x = 1/(1+x) which gives the value of x
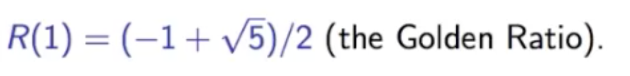
But can you find R(q) for other values of q.
(Hardy was completely stumped).
Re: BR Maths Corner-1
Apart from spelling the word Math and doing basic BODMAS, I humbly bow to all the math gurus in this thread. I never post here, but I saw this tweet and thought it may interest you guys. I have zero idea of many of the formulas below. Forgive this mango abdul for interfering in the thread.
https://twitter.com/sajaniaf/status/134 ... 64864?s=20 ---> Yesterday was Mathematics Day in remembrance of Srinivasa Ramanujan. Received this in our college WA group. As students of mathematics, each of these had special significance. Anything missing?

https://twitter.com/sajaniaf/status/134 ... 64864?s=20 ---> Yesterday was Mathematics Day in remembrance of Srinivasa Ramanujan. Received this in our college WA group. As students of mathematics, each of these had special significance. Anything missing?

Re: BR Maths Corner-1
Me too (never thought to do this before, maybe I'd have learned more if I had).Rakesh wrote:Apart from spelling the word Math and doing basic BODMAS, I humbly bow to all the math gurus in this thread.
Join the clubI never post here, but I saw this tweet and thought it may interest you guys. I have zero idea of many of the formulas below. Forgive this mango abdul for interfering in the thread.
While I'm familiar with some of the formulas in that image, it's from an engg. point of view, not math really. Never been much of a guy for pure math, the applications always seemed more interesting to me.
The attributions for a couple of those equations are typical - the "Pythagoras theorem" - even mainstream math now recognizes that this predates Pythagoras, with the current favored attribution being to the Babylonians. It is even recognized now, that Pythagoras did not even provide a proof for this theorem (that was the earlier justification for continuing to attribute it to Pythagoras, even though evidence was emerging that the theorem was known before his time), so the name "Pythagoras theorem" is just a historical artifact currently. As for calculus, that also predated Newton, and I learned from our Amber ji here, that it went by the name of "kalanam" in India centuries before Newton or Leibniz. I think this is also being recognized now, though the official attribution again goes outside India.
E=mc^2 is the equation that most people associate with relativity, but this is simply an interesting consequence of relativity (can't recall if it is a consequence of special or general relativity). The equations which actually define relativity (so far as I know) are the transformation equations from one reference frame to another (special relativity), or the tensor equation between gravity and stress (general relativity). But no denying that E=mc^2 has entered the popular imagination.
As for the rest, the equations are all certainly very influential, though personal preference will vary as to whether or not some other equations not included in the list were even more influential. For example - if the Fourier transform is deemed influential (which it most certainly is), then why not the Laplace transform (lesser known, but pretty powerful)?
Re: BR Maths Corner-1
Odd combination of equations that describe physical phenomena (MAxwell eqns. , NAvier STokes, Wave eqn, Gravitational force eqn) and those that are purely mathematical and not trying to describe any physical phenomenon- definition of i, description of logarithm etc). I would like to add Taylor series to the above for being able to give a discrete definition in an infinite series of a continuous functions- has applications in numerical methods.
Re: BR Maths Corner-1
"Odd combination" indeed and I guess different peoples' choice will be different... But still
Some formulas which I think will make top choices for many are missing here - like:
In Math - Euler's (IMO the most beautiful equation in pure math - Posted quite a few times in this dhaga)
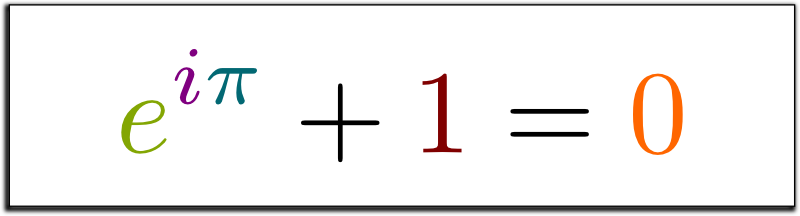
And In Physics I would include General Relativity (Einstein's Field Equation)

and Dirac's Relativistic wave equation:

(Of course many physicists who just choose "natural units" ( ħ = c = 1) write it as:

---
For me, Ramanujan still evokes awe .. for example The 'R" function (now named after "Ramanujan) I posted just a few posts above. This formula was near the end of the very first letter Ramanujan wrote to Hardy. This was beautifully recreated in the "Man who knew Infinity" movie. (I highly recommend that movie - there is a scene in the movie where Hardy is playing squash with Littlewood and wonders if that formula was sent by Littlewood as a prank).
Ramanujan introduces this function:

And out of nowhere he claims the values for some values of (q) for example:
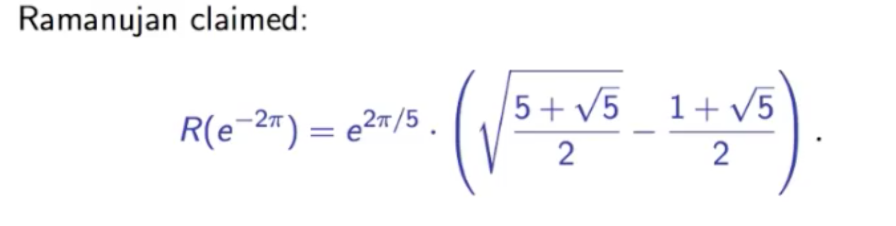
(This completely stumped Hardy. There were two/three more lines with similar results - And Hardy/Littlewood could not figure out how any one would figure that out)
(Small tidbit - Ramanujan's letter was written more than 100 years ago, result of that last line in those formulas was proved only a few years ago)
Some formulas which I think will make top choices for many are missing here - like:
In Math - Euler's (IMO the most beautiful equation in pure math - Posted quite a few times in this dhaga)
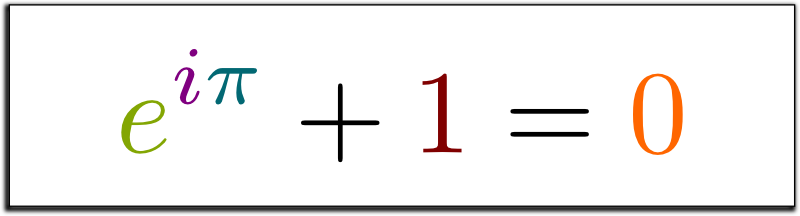
And In Physics I would include General Relativity (Einstein's Field Equation)

and Dirac's Relativistic wave equation:

(Of course many physicists who just choose "natural units" ( ħ = c = 1) write it as:

---
For me, Ramanujan still evokes awe .. for example The 'R" function (now named after "Ramanujan) I posted just a few posts above. This formula was near the end of the very first letter Ramanujan wrote to Hardy. This was beautifully recreated in the "Man who knew Infinity" movie. (I highly recommend that movie - there is a scene in the movie where Hardy is playing squash with Littlewood and wonders if that formula was sent by Littlewood as a prank).
Ramanujan introduces this function:

And out of nowhere he claims the values for some values of (q) for example:
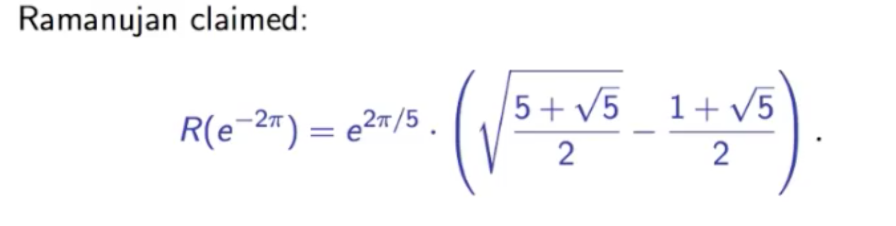
(This completely stumped Hardy. There were two/three more lines with similar results - And Hardy/Littlewood could not figure out how any one would figure that out)
(Small tidbit - Ramanujan's letter was written more than 100 years ago, result of that last line in those formulas was proved only a few years ago)
Re: BR Maths Corner-1
Speaking of National Math day: I highly recommend listening to lectures of Prof Ono, and Prof Bhargava about Ramanujan - special lecture given for this occasion. (Links are given before - and video recording is still available).
Also "Spirit of Ramanujan" (https://spiritoframanujan.com/) looks for Ramanujan type talents among young kids. So it may be worthwhile to check that out.
("We’re here to foster your passion for math and science. Ambitious, exceptional students often need resources that don’t exist in the traditional classroom. Although offers will be made on a rolling basis, we will give full consideration to complete applications received before March 1, 2021").
Also "Spirit of Ramanujan" (https://spiritoframanujan.com/) looks for Ramanujan type talents among young kids. So it may be worthwhile to check that out.
("We’re here to foster your passion for math and science. Ambitious, exceptional students often need resources that don’t exist in the traditional classroom. Although offers will be made on a rolling basis, we will give full consideration to complete applications received before March 1, 2021").
Re: BR Maths Corner-1
I was about to recommend Dirac's relativistic wave equation. Taylor Series is certainly very ubiquitous as well.
Last edited by Vayutuvan on 30 Dec 2020 06:31, edited 1 time in total.
Re: BR Maths Corner-1
^^^ Yes, Dirac's equation is as important/fundamental as any other equation I can think (eg Schrondinger's).
-
Mort Walker
- BRF Oldie
- Posts: 10372
- Joined: 31 May 2004 11:31
- Location: The rings around Uranus.
Re: BR Maths Corner-1
In the last 5-6 years there have been two movies about Indian mathematicians. I think both movies are worth watching during this covid isolation period.
Ramanujan: 2015 "The Man Who Knew Infinity" starring Dev Patel and Jeremy Irons. It was a decent film, but they could have gone more into showing how Ramanujan thought through mathematics. It focuses a lot on Ramanujan and Hardy's friendship.
Shakuntala: 2020 "Shakuntala Devi" starring Vidya Balan. This film had the potential to be great, but is ruined because it presented as a Bollywood masala picture. Vidya Balan did a decent acting job though.
Ramanujan: 2015 "The Man Who Knew Infinity" starring Dev Patel and Jeremy Irons. It was a decent film, but they could have gone more into showing how Ramanujan thought through mathematics. It focuses a lot on Ramanujan and Hardy's friendship.
Shakuntala: 2020 "Shakuntala Devi" starring Vidya Balan. This film had the potential to be great, but is ruined because it presented as a Bollywood masala picture. Vidya Balan did a decent acting job though.
Re: BR Maths Corner-1
I liked (really liked) "The man who knew infinity" because like no other movie this portrayed mathematics very accurately. The equations written on paper, or on black board or spoken were all beautifully carried out the math part. This is why most mathematicians really love the movie and admire the care the director took to make that part very enjoyable.
This was due to the fact that the chief mathematical advisers for the movie (who had a really big hand and the director listened to them) were none other than Manjul Bhargava (Fields Medal - India's first, Padma Bhusan, Infosys prize - Modi's first invite to India for GIAN's scheme etc) and Ken Ono (world renowned number theorist). When Dev Patel writes that beautiful elliptical function equation (making his professor stumped) in the class - he spent hours training with Ono - to write all the symbols correctly and fast and smoothly - without any error as Ramanujan would have written. Truly remarkable. (I was really impressed).
Similarly Taxi-cab number 1729 etc was the actual number (smallest such number) which can be written as sum of two cubes in two different ways. (10^3+9^3 = 12^3+1^3 = 1729).
(BTW - some math behind taxi-cab numbers and elliptical integrals and prime numbers inspired by Ramanujan has been discussed in this thread - If I may say so, there is some good math here )..
)..
Hardy, Littlewood were played excellently and Cambridge scenes were quite good. The film spends much less time in India and I wish costumes and scenes in India were more authentic - may be they should have picked a good bollywood established actor and costume designer - in my humble opinion. But overall I liked the movie. The book is quite good and I highly recommend it as the book has more details about Ramanujan's time in India than the movie does.
(I took my whole family to see the movie when it just came out in theaters - Of course, I knew a lot about making of this movie. There was one scene in the release I saw where Hardy misspells "Jacobi" on the board - thankfully they reshot the scene and in later versions of the movie this error is not there )
)
---
One scene I liked - when Hardy talks to Ramnujann in the great hall and tells him that one day his place there will be with other greats like Newton. Exactly hundred years later after Ramanujan became a Fellow of Royal Society - This happened, and among people celebrating that event were worlds leading celebrities including George Andrews, Manjul Bhargava, Ken Ono and host of other mathematicians from all parts of the world. 100 years after the first Indian who became the first FRS in science, the President of the Royal Society this time, who was presiding over the ceremony was Indian(! Venkatraman "Venki" Ramakrishnan (Nobel Prize). Ramakrishnan was actually crying when he started speaking.
This was due to the fact that the chief mathematical advisers for the movie (who had a really big hand and the director listened to them) were none other than Manjul Bhargava (Fields Medal - India's first, Padma Bhusan, Infosys prize - Modi's first invite to India for GIAN's scheme etc) and Ken Ono (world renowned number theorist). When Dev Patel writes that beautiful elliptical function equation (making his professor stumped) in the class - he spent hours training with Ono - to write all the symbols correctly and fast and smoothly - without any error as Ramanujan would have written. Truly remarkable. (I was really impressed).
Similarly Taxi-cab number 1729 etc was the actual number (smallest such number) which can be written as sum of two cubes in two different ways. (10^3+9^3 = 12^3+1^3 = 1729).
(BTW - some math behind taxi-cab numbers and elliptical integrals and prime numbers inspired by Ramanujan has been discussed in this thread - If I may say so, there is some good math here
Hardy, Littlewood were played excellently and Cambridge scenes were quite good. The film spends much less time in India and I wish costumes and scenes in India were more authentic - may be they should have picked a good bollywood established actor and costume designer - in my humble opinion. But overall I liked the movie. The book is quite good and I highly recommend it as the book has more details about Ramanujan's time in India than the movie does.
(I took my whole family to see the movie when it just came out in theaters - Of course, I knew a lot about making of this movie. There was one scene in the release I saw where Hardy misspells "Jacobi" on the board - thankfully they reshot the scene and in later versions of the movie this error is not there
---
One scene I liked - when Hardy talks to Ramnujann in the great hall and tells him that one day his place there will be with other greats like Newton. Exactly hundred years later after Ramanujan became a Fellow of Royal Society - This happened, and among people celebrating that event were worlds leading celebrities including George Andrews, Manjul Bhargava, Ken Ono and host of other mathematicians from all parts of the world. 100 years after the first Indian who became the first FRS in science, the President of the Royal Society this time, who was presiding over the ceremony was Indian(! Venkatraman "Venki" Ramakrishnan (Nobel Prize). Ramakrishnan was actually crying when he started speaking.
-
Mort Walker
- BRF Oldie
- Posts: 10372
- Joined: 31 May 2004 11:31
- Location: The rings around Uranus.
Re: BR Maths Corner-1
AmberG,
Thanks for the backgrouund info. In 1988, there was a PBS Nova special called "The Man Who Loved Numbers" which was about Ramanujan. I thought this was a good short 1 hour documentary.
Thanks for the backgrouund info. In 1988, there was a PBS Nova special called "The Man Who Loved Numbers" which was about Ramanujan. I thought this was a good short 1 hour documentary.
Re: BR Maths Corner-1
Mort ji,
Is it about Paul Erdos? There is a biography of Erdos titled "The Man Who Loved Only Numbers". Ramanujan's biography is called "The Man Who Knew Infinity" which is made into a flaccid movie of the same name.
Both are great books.
Is it about Paul Erdos? There is a biography of Erdos titled "The Man Who Loved Only Numbers". Ramanujan's biography is called "The Man Who Knew Infinity" which is made into a flaccid movie of the same name.
Both are great books.
Last edited by Vayutuvan on 03 Jan 2021 06:08, edited 1 time in total.