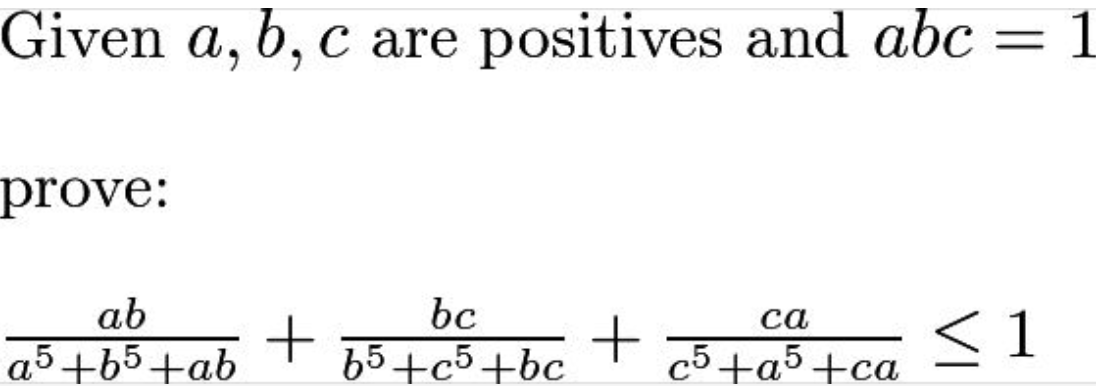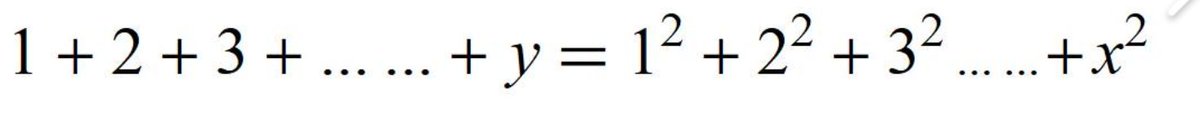Page 47 of 60
Re: BR Maths Corner-1
Posted: 09 Jun 2020 06:05
by Vayutuvan
Amber G. wrote:Just for fun:
Two problems, if you like to find any elegant methods to solve, or to challenge others:
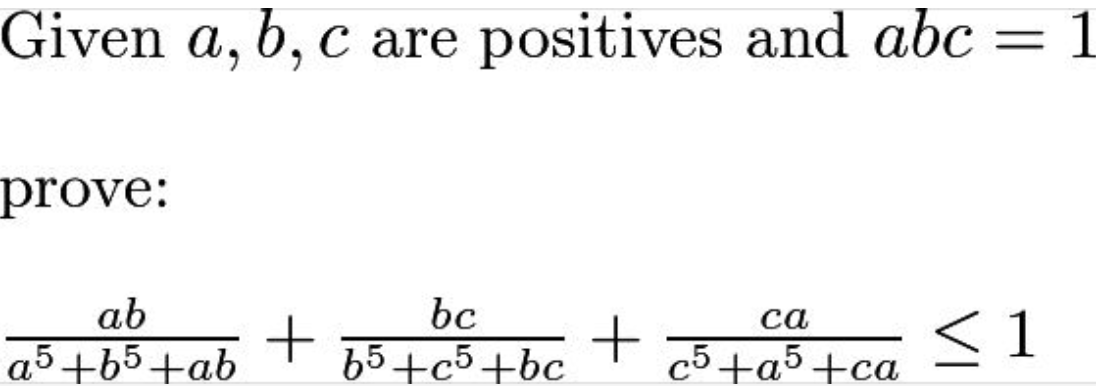
Somewhat harder: For number theorists (or computer programmers)
Sum of the first 'y' natural numbers = Sum of the squares of the first 'x' natural numbers.
Are there any solutions (in positive integers) other than x=y=1?
If so how many?
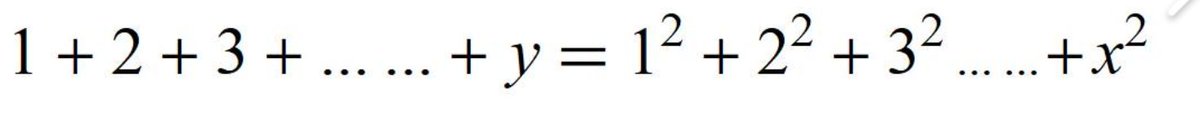
For the second problem, my guess trivial solution of x = y = 1 is the only solution.
May be simple graphing of the two polynomials
y(y+1)/2 and x(x+1)(2x+1)/3 on an integer lattice might do it.
Re: BR Maths Corner-1
Posted: 09 Jun 2020 23:14
by sudarshan
Vayutuvan wrote:
For the second problem, my guess trivial solution of x = y = 1 is the only solution.
May be simple graphing of the two polynomials
y(y+1)/2 and x(x+1)(2x+1)/3 on an integer lattice might do it.
I will subject you to death by counter-example

. Try (x=5, y=10) and (x=6, y=13). BTW, I think you meant x(x+1)(2x+1)/6.
Re: BR Maths Corner-1
Posted: 10 Jun 2020 01:17
by Amber G.
sudarshan wrote:Vayutuvan wrote:
For the second problem, my guess trivial solution of x = y = 1 is the only solution.
May be simple graphing of the two polynomials
y(y+1)/2 and x(x+1)(2x+1)/3 on an integer lattice might do it.
I will subject you to death by counter-example

.
Try (x=5, y=10) and (x=6, y=13). BTW, I think you meant x(x+1)(2x+1)/6.
.
Nice! (There are still more cases of "death by counter-example"

! eg
x=85)
Re: BR Maths Corner-1
Posted: 10 Jun 2020 07:48
by sudarshan
Amber G. wrote:
Nice! (There are still more cases of "death by counter-example"

! eg
x=85)
Yeah I'm finding more by brute force - (x=85, y=645) is another one, but not getting a general solution. Hint?
Re: BR Maths Corner-1
Posted: 11 Jun 2020 04:27
by Vayutuvan
sudarshan wrote:Vayutuvan wrote:
For the second problem, my guess trivial solution of x = y = 1 is the only solution.
May be simple graphing of the two polynomials
y(y+1)/2 and x(x+1)(2x+1)/3 on an integer lattice might do it.
I will subject you to death by counter-example

. Try (x=5, y=10) and (x=6, y=13). BTW, I think you meant x(x+1)(2x+1)/6.
Yes. x(x+1)(2x+1)/6.
(wrong stuff deleted) Bezout's theorem applies to homogeneous polynomials only.
Re: BR Maths Corner-1
Posted: 11 Jun 2020 05:48
by Vayutuvan
https://en.wikipedia.org/wiki/Elliptic_ ... ral_points
Integral points
This section is concerned with points P = (x, y) of E such that x is an integer.[17] The following theorem is due to C. L. Siegel: the set of points P = (x, y) of E(Q) such that x is an integer is finite. This theorem can be generalized to points whose x coordinate has a denominator divisible only by a fixed finite set of prime numbers.
The theorem can be formulated effectively. For example,[18] if the Weierstrass equation of E has integer coefficients bounded by a constant H, the coordinates (x, y) of a point of E with both x and y integer satisfy:
{\displaystyle \max(|x|,|y|)<\exp \left(\left[10^{6}H\right]^{{10}^{6}}\right)}\max(|x|,|y|)<\exp \left(\left[10^{6}H\right]^{{10}^{6}}\right)
For example, the equation y2 = x3 + 17 has eight integral solutions with y > 0 :[19]
(x, y) = (−1, 4), (−2, 3), (2, 5), (4, 9), (8, 23), (43, 282), (52, 375), (5234, 378661).
As another example, Ljunggren's equation, a curve whose Weierstrass form is y2 = x3 − 2x, has only four solutions with y ≥ 0 :[20]
(x, y) = (0, 0), (−1, 1), (2, 2), (338, 6214).
Brute force computer program can stop at testing for
x <= exp( [3*10^6]^(10^6))
y <= exp( [3*10^6]^(10^6))
since the coefficients are bounded by 3.
Re: BR Maths Corner-1
Posted: 11 Jun 2020 23:58
by Vayutuvan
I went through the statement of Bezout's theorem. So we can use the theorem to put an upper bound of 6 intersection points with multiplicities. We can stop after the above bound given by Seigel or six such points are found. Asymptotically speaking, the cubic grows faster than the quadratic.
My assumption that cubic is monotonically non-decreasing is incorrect.
The problem boils down to finding zeros of z = x(x+1)(2x+1) - 2y(2y+1)
Mya be this particular problem has an easier solution than doing brute force enumeration is the question @AmberG sir is asking, I suppose.
Re: BR Maths Corner-1
Posted: 12 Jun 2020 00:55
by Amber G.
Saw this -

... May this bring a smile


Re: BR Maths Corner-1
Posted: 12 Jun 2020 03:15
by Vayutuvan
https://books.google.com/books?id=dZh2S ... &q&f=false
In the lighter vein, here is one page from the book "Mathematical Apocrypha: Stories and Anecdotes of Mathematicians and their ..." By Steven Krantz.
I found the book to be quite enjoyable. It is somewhat similar to "Surely You Are Joking, Mr. Feynman".
Re: BR Maths Corner-1
Posted: 12 Jun 2020 03:24
by Vayutuvan
Re: BR Maths Corner-1
Posted: 13 Jun 2020 02:28
by Vayutuvan
sudarshan wrote:Amber G. wrote:
Nice! (There are still more cases of "death by counter-example"

! eg
x=85)
Yeah I'm finding more by brute force - (x=85, y=645) is another one, but not getting a general solution. Hint?
Could there be a pattern in the factoring x and y into their prime components)
(5,10) is (5^1, 2*5)
(6,13) is
either (5^1+1, 13) or (2*3, 13)
(85, 645) is (5^1*17, 3*5*43)
...
Try x of the form 2^m * 3^n or 5*n?
We need x(x+1)(2x+1) to be divisible by 6.
if there is a common factor between y(y+1)/2 and x(x+1)(2x+1) it cannot be a multiple of 6, i.e. 2*3
else
x even: 3 | (x+1)(2x+1) or 6 | x
x odd: 3 | x(2x+1) or 6 | (x+1)
y even: 3 | (y+1)
y odd: 3 | y
...
(later)
I don't think case analysis is the way to go. :-(
Re: BR Maths Corner-1
Posted: 14 Jun 2020 20:29
by sudarshan
^ Yes I'm not able to get a handle on a general way of solving this, and AmberG not giving hint onlee. How about the other problem, the supposedly easier abc=1 thingy?
Re: BR Maths Corner-1
Posted: 16 Jun 2020 20:47
by chilarai
Vayutuvan wrote:
We need x(x+1)(2x+1) to be divisible by 6.
x(x+1)(2x+1) is always divisible by 6 isn't it since the quotient is equal to 1^2 + 2^2 ...x^2
or am i missing something obvious
only thing i get is
3y(y+1)/ x(x+1) = 2x+1 i.e a whole number . so looks like if y(y+1) is divisible by x(x+1) then that is one possible criteria ( may not be sufficient )..
other solution is when x(x+1)/3 divides y(y+1)
Re: BR Maths Corner-1
Posted: 16 Jun 2020 22:56
by Amber G.
Honoring the centenary of Ramanujan's death, in the April issue of New Scientists, there is a nice article by Ken Ono & Robert Schneider.
Srinivisa Ramanujan's mathematics seemed to come from a parallel universe and we are still trying to understand it today
Link:
Dreamy mathematics
This article may not be accessible to non-subscribers, and is behind a pay-wall so I am posting a readable copy for brf-readers use only.
<pdf image of above article >
Re: BR Maths Corner-1
Posted: 17 Jun 2020 02:37
by Amber G.
Will post later but a few short comments on some comments here ..
Vayutuvan wrote: .. So we can use the theorem to put an upper bound of 6 intersection points with multiplicities. We can stop after the above bound given by Seigel or six such points are found.
Hmm ..What does this mean? In any case don't we already have more than six points (if we allow 0 and negatives as our Indian mathematicians say those are numbers too) pairs of (x,y) (0,0), (0, -1), (1,1), (1, -2), (5,10), (5,-11), (6,13), (6,-14).. ityadi ityadi...
...
chilarai wrote:
x(x+1)(2x+1) is always divisible by 6 isn't it since the quotient is equal to 1^2 + 2^2 ...x^2
or am i missing something obvious
Right! Of course. t
wo consecutive integers (x and (x+1)) - one of them must be even so must be divisible by 2 and among (2x, 2x+1, 2x+2) -- three consecutive numbers -- one must be divisible by 3. (Of course if 2x is divisible by 3, so is x and same argument for 2x+2. (Besides, as you said, the sum has to be an integer)
---
Has anyone found a solution larger than x=85?
---
About abc=1 thingie - the problem was sent to me by my niece (middle school) over whatsapp..looking for elegant method which a middle schooler can follow/appreciate..(I liked the problem because it gave me a chance to teach a nice property/theorem which is generally not covered in regular high-school math course ).
(Hint:
what if the problem is changed to abc=1, prove
1/(1+a^3+b^3)+ 1/(1+b^3+c^3)+1/(1+c^3+a^3) <= 1)
Re: BR Maths Corner-1
Posted: 17 Jun 2020 02:48
by Vayutuvan
chilarai wrote:Vayutuvan wrote:
We need x(x+1)(2x+1) to be divisible by 6.
x(x+1)(2x+1) is always divisible by 6 isn't it since the quotient is equal to 1^2 + 2^2 ...x^2
That is what I am saying.
We know
1. y(y+1)/2 is a whole number
2. x(x+1)(2x+1)/6 is a whole number
3. y(y+1) = x(x+1)(2x+1)/3
Then I made the following table to see if there is some pattern
Code: Select all
(y+0)(y+1) (x+0)(x+1)(2x+1)
(y+1)(y+2) (x+1)(x+2)(2x+3)
(y+2)(y+3) (x+2)(x+3)(2x+5)
(y+3)(y+4) (x+3)(x+4)(2x+7)
(y+4)(y+5) (x+4)(x+5)(2x+9)
(y+5)(y+6) (x+5)(x+6)(2x+11)
(y+6)(y+7) (x+6)(x+7)(2x+13)
(y+7)(y+8) (x+7)(x+8)(2x+15)
(y+8)(y+9) (x+8)(x+9)(2x+17)
(y+9)(y+10) (x+9)(x+10)(2x+19)
(y+10)(y+11) (x+10)(x+11)(2x+21)
(y+11)(y+12) (x+11)(x+12)(2x+23)
... (x+12)(x+13)(2x+25)
Now let us look at the known solutions
(0,0), (0, -1), (1,1), (1, -2), (5,10), (5,-11), (6,13), (6,-14), ..., (85,645), (85, -2^m.3^n*k-645)
for some whole numbers m, n, and k?
Re: BR Maths Corner-1
Posted: 17 Jun 2020 04:00
by Amber G.
Vayutuvan wrote: ....
That is what I am saying. Since x(x+1)(2x+1) is always divisible by 2*3, either y(y+1) either y or y+1 is divisible by 3.
hmm .. y=10 is a solution.. neither y or nor y+1 is divisible by 3. (Not to mention, y=1 etc)..
Re: BR Maths Corner-1
Posted: 17 Jun 2020 05:28
by Vayutuvan
Amber G. wrote:Vayutuvan wrote: ....
That is what I am saying. Since x(x+1)(2x+1) is always divisible by 2*3, either y(y+1) either y or y+1 is divisible by 3.
hmm .. y=10 is a solution.. neither y or nor y+1 is divisible by 3. (Not to mention, y=1 etc)..
Yes. But that is covered by @chillarai and my post previous to that which says that there is a common factor of 5 which is the case is the two solutions (x,y) = {(5,10), (85, 645), ...}
Can we guess the next solutions in that sequence?
Let us look at it slightly from quadratic equation side.
Let us assume that x(x+1)(2x+1)/3 = m. Fre the time being assume that we are looking for solutions where x > 0, i.e. x positive --> m positive.
Quadratic equation is
y^2 + y - m = 0
Discriminant: 1 + 4m which is positive. So we have two real roots. Since we are looking for positive roots,
y = (-1 + sqrt(1+4m))/2
Let 3y(y+1) = n
Then we get a cubic of the form
2x^3 + 3x^2+ x - n = 0
solve for x ...
and then what?
Re: BR Maths Corner-1
Posted: 17 Jun 2020 20:53
by Amber G.
I am putting simplified version of the above 2 problems - uses the same/similar ideas and math (or computer programming) techniques. (These problems are a bit simpler than the first two so may be more fun and less work)
1.
given a,b,c are positive numbers and abc = 1
prove (1/(1+a^3+b^3)) + (1/(1+b^3+c^3)) + (1/(1+c^3+a^3)) <= 1
***
2.
(x, y are positive integers)
1+2+.....y = x^2
What are the other solutions, (other than trivial x=y=1 ) .. (Hint: there is one x=6 and y=8).
Re: BR Maths Corner-1
Posted: 18 Jun 2020 02:08
by Vayutuvan
3y(y+1) = 2x^3 + 3x^2 + x
can be put into this form
y^2 - x^2 = (2/3) x^3 + (1/3) x - y
LHS is a hyperbola of a special kind. it is the conjugate of a unit hyperbola.
In RHS the (-y) term is a little bit of a problem but it is a cubic when on the line y = k.
I can't think in modulo arithmetic but more comfortable in the real field setting. On top of that, I think in algorithmically terms.

One way to do these kinds of problems is to use a method called relaxation which is very popular in the domain of Combinatorial Optimization (and cryptanalysis).
Re: BR Maths Corner-1
Posted: 18 Jun 2020 02:55
by Vayutuvan
Amber G. wrote:Will post later but a few short comments on some comments here ..
Vayutuvan wrote: .. So we can use the theorem to put an upper bound of 6 intersection points with multiplicities. We can stop after the above bound given by Seigel or six such points are found.
Hmm ..What does this mean? In any case don't we already have more than six points (if we allow 0 and negatives as our Indian mathematicians say those are numbers too) pairs of (x,y) (0,0), (0, -1), (1,1), (1, -2), (5,10), (5,-11), (6,13), (6,-14).. ityadi ityadi...
The solution is periodic two periods of 1 and 6, very roughly speaking.
Re: BR Maths Corner-1
Posted: 18 Jun 2020 05:07
by Vayutuvan
Amber G. wrote:I am putting simplified version of the above 2 problems - uses the same/similar ideas and math (or computer programming) techniques. (These problems are a bit simpler than the first two so may be more fun and less work)
1.
given a,b,c are positive numbers and abc = 1
prove (1/(1+a^3+b^3)) + (1/(1+b^3+c^3)) + (1/(1+c^3+a^3)) <= 1
***
2.
(x, y are positive integers)
1+2+.....y = x^2
What are the other solutions, (other than trivial x=y=1 ) .. (Hint: there is one x=6 and y=8).
2.
y = \tan^2(\theta); x = \sin(\frac{\pi}{4}) \tan(\theta) \sec(\theta)
(corrected) This should work.
Added later:
Another solution in terms of hyperbolic functions is as follows.
y = \csch^2(u); x = \frac{1}{\sqrt 2} \csch(u) coth(u)
or simpler
y = \sinh^2(u); x = \frac{1}{2 \sqrt 2} \sinh(2u)
Now what?
Re: BR Maths Corner-1
Posted: 18 Jun 2020 05:57
by sudarshan
The second problem (easier version) reduces to finding all positive numbers "a" such that:
2*a^2+1 is a perfect square
(OR)
2*a^2-1 is a perfect square
For any such a:
for the first case, y=2*a^2, x=a*sqrt(2*a^2+1)
for the second case, y=2*a^2-1, x=a*sqrt(2*a^2-1)
Now if only I knew how to find all those "a" values in a general way.
Specific solutions by brute force:
a=1 => y=1, x=1 (second case)
a=2 => y=8, x=6 (first case)
a=5 => y=49, x=35 (second case)
a=12 => y=288, x=204 (first case)
a=29 => y=1681, x=1189 (second case)
a=70 => y=9800, x=6930 (first case)
a=169 => y=57121, x=40391 (second case)
Etc.
I can see the pattern here - each value of a is twice the previous value of a, plus the previous-previous value of a.
I.e.,
(Trivial solution a=0, y=0, x=0)
First a = 1-------------------------Case 2----y=1----x=1
Next a = 2*1 + 0 = 2----------------------Case 1----y=8----x=6
Next a = 2*2 + 1 = 5----------------------Case 2----y=49----x=35
Next a = 2*5 + 2 = 12----------------------Case 1----y=288----x=204
Next a = 2*12 + 5 = 29----------------------Case 2----y=1681----x=1189
Next a = 2*29 + 12 = 70----------------------Case 1----y=9800----x=6930
Next a = 2*70 + 29 = 169----------------------Case 2----y=57121----x=40391
Next a = 2*169 + 70 = 408----------------------Case 1----y=332928----x=235416
Next a = 2*408 + 169 = 985----------------------Case 2----y=1940449----x=1372105
Next a = 2*985 + 408 = 2378----------------------Case 1----y=11309768----x=7997214
Next a = 2*2378 + 985 = 5741----------------------Case 2----y=65918161----x=46611179
Next a = 2*5741 + 2378 = 13860----------------------Case 1----y=384199200----x=271669860
Next a = 2*13860 + 5741 = 33461----------------------Case 2----y=2239277041----x=1583407981
Next a = 2*33461 + 13860 = 80782----------------------Case 1----y=13051463048----x=9228778026
.
.
.
(To infinity I guess)
But why is this pattern this way?
Re: BR Maths Corner-1
Posted: 18 Jun 2020 07:08
by Vayutuvan
sudarshan ji,
it looks like there is recurrence relation in there somewhere. have you tried 2^2^2^... k ...^2, i.e a k-tower - let us call it tower(2,k) and tower(2,k) - 1? may be fermats little theorem is applicable here. I am sort of tired. number theory is like smoking, very hard to give up. I am trying.
Re: BR Maths Corner-1
Posted: 18 Jun 2020 09:29
by Amber G.
sudarshan wrote:The second problem (easier version) reduces to finding all positive numbers "a" such that:
2*a^2+1 is a perfect square
(OR)
2*a^2-1 is a perfect square
For any such a:
for the first case, y=2*a^2, x=a*sqrt(2*a^2+1)
for the second case, y=2*a^2-1, x=a*sqrt(2*a^2-1)
Now if only I knew how to find all those "a" values in a general way.
<The pattern (0.0)(1,1),(6,8),(35,49)(204,288) .... etc...>
But why is this pattern this way?
Excellent!
Now the pattern, say for x is given by x_n = 6*x_(n-1) - x_(n-2)
In other words, if first value of x=0, and second value = 1 , then the
next one is
6*1 - 0 =6
Next value is
6*6 -1 = 35
Next one is
6*35 - 6 = 204
Next one is
6*204 - 35 etc....
And so on..
(This is not hard to prove, and I will show it fairly soon later in the post - proof can be seen in any good book too - look up "Pell's equation" (the correct name ought to be Brhamgupta equation) also there are problems here in Brf dhaga similar to this where the proof is given ).
----
The interesting anecdote - some one asked Ramanujan a similar problem while he was taking a walk - Ramanujan, of course, answered it immediately. The answer was many digits long yet he answered it almost right-away- without even a paper or pen. His friend was really surprised (his friend was also quite a good Indian mathematician who was also studying in Cambridge and heard that problem) to see this. He asked how did Ramanujan do it so quickly - (The standard method using Pell's equation does require more than a few seconds) .. Ramanujan answered - " He knew the answer is related to continued fraction of sqrt(2).
Now sqrt(2) = 1 / (2+1 /( 2+ 1/ + ---) or:
<see graphics here>or wiki for article on continued fraction. (eg:
https://en.wikipedia.org/wiki/Square_ro ... esentation
Or IOW: the approximation for sqrt(2) by expanding this continued fraction, you get the fractions ..
are
1/1, 3/2, 7/5, 17/12, 41/29, 99/50 ....
Each fraction in the series is a better approx of sqrt(s)
Now if you multiplied denominator and numerator (eg 3*2=6, 7*5=35, 17*12 you get successive values of x)
So above is the continued fraction method.
(Intuitively - as Ramanujan will say . you if you want 2*a^2 +-1 = b^2 the ratio of b and a is nearly sqrt(2)..so if working with integers, the continued fraction of sqrt(2) is the way to go).
****
Now if you want explicit formula here choose any integer n
x = ((3+2 √ 2)^n - (3 - 2 √ 2)^n) / (4 √ 2)
y = ((3+2 √ 2) ^n + (3 - 2 √ 2) ^n - 2)/ 4
It's easy to put in the computer, (easy to verify that x and y both are integers and has the required property).
****
Hope people find it fun,
Re: BR Maths Corner-1
Posted: 18 Jun 2020 09:48
by Amber G.
First a = 1-------------------------Case 2----y=1----x=1
Next a = 2*1 + 0 = 2----------------------Case 1----y=8----x=6
Next a = 2*2 + 1 = 5----------------------Case 2----y=49----x=35
Next a = 2*5 + 2 = 12----------------------Case 1----y=288----x=204
Next a = 2*12 + 5 = 29----------------------Case 2----y=1681----x=1189
Next a = 2*29 + 12 = 70----------------------Case 1----y=9800----x=6930
Next a = 2*70 + 29 = 169----------------------Case 2----y=57121----x=40391
Next a = 2*169 + 70 = 408----------------------Case 1----y=332928----x=235416
Next a = 2*408 + 169 = 985----------------------Case 2----y=1940449----x=1372105
Next a = 2*985 + 408 = 2378----------------------Case 1----y=11309768----x=7997214
Next a = 2*2378 + 985 = 5741----------------------Case 2----y=65918161----x=46611179
Next a = 2*5741 + 2378 = 13860----------------------Case 1----y=384199200----x=271669860
Next a = 2*13860 + 5741 = 33461----------------------Case 2----y=2239277041----x=1583407981
Next a = 2*33461 + 13860 = 80782----------------------Case 1----y=13051463048----x=9228778026
.
.
.
(To infinity I guess)
But why is this pattern this way?
Sudarshanji - As I said above (or look up wiki article about continued fraction for squrt(2)...
Since, the continued fraction of sqrt(2) is 1+ 1/(2+ 1/ (2+ .... You get the numbersL
1/1, 3/2, 7/5, 17/12 ...
The pattern here is next numerator(or denominator) is 2* previous one + 1 * previous to previous one ... eg:
7=2*3+1
17=2*7+3 ...
This comes because the continued fraction numbers are [1,2] ...
By the way this method works for other similar equation(s)... all you have to do is to find continued fraction which is not hard. (NO it will *not* work for the first version of the problem - which is quite a bit harder, but it will work for many quadratic equations where you want to find integer solutions)
****
One thing I try to do when I teach or whenever I get a chance is to call the Pell equation as Brahmgupta-Pell equation as Brhamgupta has documented it centuries before Pell.
The Continued Fractions are taught is India but is not that popular here in the west. The theory of continued fraction was one of Ramnujan's interest.
Re: BR Maths Corner-1
Posted: 20 Jun 2020 08:03
by sudarshan
^ I took a look at the continued fractions, very interesting. To instantly intuit a solution on that basis requires one to be directly plugged into the matrix and receiving instant feeds methinks

. What that man could have done if he'd lived longer!
But is there a formal solution?
Re: BR Maths Corner-1
Posted: 22 Jun 2020 04:01
by Vayutuvan
sudarshan wrote:^ I took a look at the continued fractions, very interesting. To instantly intuit a solution on that basis requires one to be directly plugged into the matrix and receiving instant feeds methinks

. What that man could have done if he'd lived longer!
But is there a formal solution?
In general, there is no general solution method for diophantine equations. That was Hilbert's 10th problem whose statement I am including below. (1)
Hilbert's tenth problem is the tenth on the list of mathematical problems that the German mathematician David Hilbert posed in 1900. It is the challenge *to provide a general algorithm which, for any given Diophantine equation (a polynomial equation with integer coefficients and a finite number of unknowns), can decide whether the equation has a solution with all unknowns taking integer values.*
Three collaborators Martin Davis (student of Alonzo Church, just like Turing), Hillary Putnam (a philosopher), and Julia Robinson worked on the problem for 20 starting in 1944. They made a lot of headway but were unable to resolve the question. In 1970, Yuri Matiyasevich, a Russian who then was barely in his 20s, drew heavily on the partial results obtained by the people mentioned above, had finally proved that no such algorithm is possible. In other words, he showed that that the question asked in "The Hilbert's Tenth Problem" is undecidbale. The original idea of this line of attack came from Emil Post. Emile Post proposed a computaional model named as Post's Machine (also called Post-Turing Machine) in a paper called Fotmulation 1. He then came up with a problem knwon as Post Correspodence Problem and showed that it is undecidable. This is equivalent to Turing Machine and The Halting Problem.
To summarize, informally speaking, Matiyasevch showed that the Halting Problem can be reduced to solving a diophantine equation. Since Halting Problem is known to be undecidable, so is the diophantine equation problem.
MIT Press has published a monogram called "Hibert's Tenth Problem" by Matiyasevich (2) in which Matisevich gives the proof in its gory detail along with applications of his proof method.
It is a very lucid account of all the results of Robinson, Davis, Putnam, and his own contributions which resolves the Hilberts Tenth Problem in the negative. The theorem is called Matisyasevich's theorem or now MRDP (Matiyasevic-Robinson-Davis-Putnam) Theorem.
I highly recommend the book to anybody interested in how some of the problems in Logic are attacked.
-----
Foot notes:
1. Wikipedia page is
here
2.
Hilbert's 10th Problem By Yuri Matiyasevich: This book presents the full, self-contained negative solution of Hilbert's 10th problem
Look at the reviews of the book at
https://www.amazon.com/dp/0262132958/.
A 26 page paper by Prof. Matiyasevich is here
https://www.academia.edu/19447022/HILBE ... vich/]here.
Re: BR Maths Corner-1
Posted: 22 Jun 2020 05:24
by Vayutuvan
A follow up post to the above.
What it means is that every Diophantine Equation or systems of equations need their own specific method to solve. There is no way to know at the outset whether a solution exists.
That is why solutions to Dophantine Equations are used as keys in public-key cryptography or asymmetric key cryptography. Cryptanalysis is made hard due to the fact that there is no general algorithm to derive the private key from the public key. On the other hand, if there is a simple recursive equation as above or the period is short, then key pairs derived from such a diophantine equation are amenable to cryptanalysis by entities who have modest compuational resources. Partial decoding is possible some times using Relaxation methods.
Re: BR Maths Corner-1
Posted: 23 Jun 2020 09:52
by sudarshan
Vayutuvan wrote:
In general, there is no general solution method for diophantine equations. That was Hilbert's 10th problem whose statement I am including below. (1)
...
So that means the cubic problem (the harder version of problem 2) also has no general solution? I've come across the term "Diophantine equations" before, but I think that was in a very specific case, and there was also a way to solve (there would be multiple solutions). Whereas what you posted above seems to be a much broader class of problems, under the umbrella term of "Diophantine."
As an anecdote, a friend of mine, while taking a math course at a US university, had this professor, who introduced the term "Diophantine equations" but said "they are also called Aryabhatta equations, I have no clue why." My friend informed him that Aryabhatta was an Indian mathematician. The wiki entry on Diophantine equations doesn't mention Aryabhatta, but there are other wiki entries (I think the one on Aryabhatta himself) which mention that he preceded Diophantus by 250 years (according to the standard dating - of course there was gross distortion of dates in Indian history during the colonial era). The solution technique he came up with was "kuttaka" (pulverization) - repeatedly reducing the problem to smaller and smaller divisors, maybe that also applies to one specific class of Aryabhatta equations.
Re: BR Maths Corner-1
Posted: 23 Jun 2020 15:24
by Schmidt
chilarai wrote:Vayutuvan wrote:
We need x(x+1)(2x+1) to be divisible by 6.
x(x+1)(2x+1) is always divisible by 6 isn't it since the quotient is equal to 1^2 + 2^2 ...x^2
or am i missing something obvious
only thing i get is
3y(y+1)/ x(x+1) = 2x+1 i.e a whole number . so looks like if y(y+1) is divisible by x(x+1) then that is one possible criteria ( may not be sufficient )..
other solution is when x(x+1)/3 divides y(y+1)
----------------------
(2x+1) can be written as (x+2) + (x-1) and each product with first 2 terms will be divisible by 6 as they are 3 consecutive nos
Re: BR Maths Corner-1
Posted: 23 Jun 2020 15:31
by Schmidt
Vayutuvan wrote:Amber G. wrote:Just for fun:
Two problems, if you like to find any elegant methods to solve, or to challenge others:
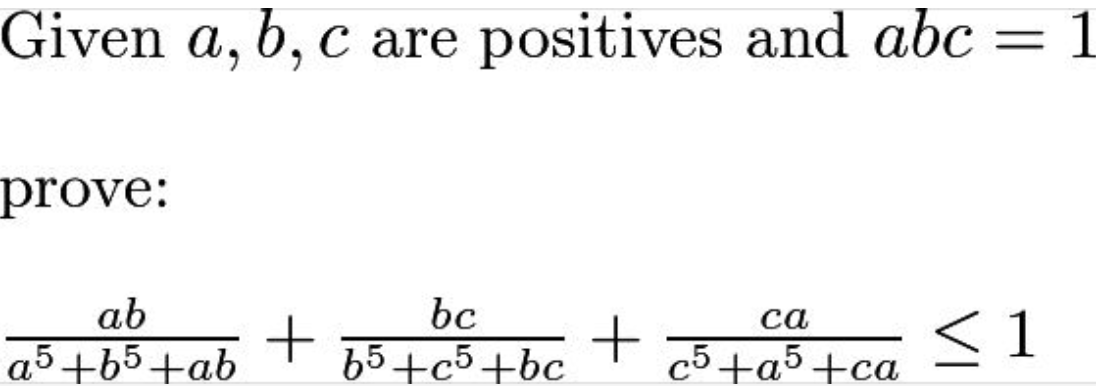
Somewhat harder: For number theorists (or computer programmers)
Sum of the first 'y' natural numbers = Sum of the squares of the first 'x' natural numbers.
Are there any solutions (in positive integers) other than x=y=1?
If so how many?
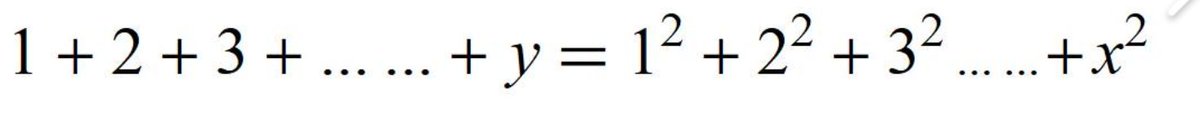
For the second problem, my guess trivial solution of x = y = 1 is the only solution.
May be simple graphing of the two polynomials
y(y+1)/2 and x(x+1)(2x+1)/3 on an integer lattice might do it.
±++++++++++++++++++++
The first problem can be solved by taking a^5 , b^5, ab as three terms and use AM > GM, likewise for remaining 2 terms and add up
Same for the similar problem that Amber G gave later
Use a^3 , b^3 ,1 as three terms and AM > GM
Re: BR Maths Corner-1
Posted: 23 Jun 2020 21:46
by Amber G.
Schmidt wrote:
Same for the similar problem that Amber G gave later
Use a^3 , b^3 ,1 as three terms and AM > GM
Can you expand? (Thanks in advance). (Of course, others can comment too).
--
Background - The problem came to my attention as one niece sent that to me. She is quite bright (her parents, uncles and grandfather include graduates and math professors

) yet was not finding any easy way to solve it. Obviously she (and others) tried AM>GM and other techniques one learns but it came close but not quite. (She could easily prove a^3+b^+1 >=3ab = 3/c or 1/(a^3+b^3+1) <= c/3 but then what? )
(The problem my niece sent was with the terms a^5+b^5+..... The a^3+b^3+1 problem I made it up to show the concept I was trying to teach her using simpler terms).
Re: BR Maths Corner-1
Posted: 23 Jun 2020 22:04
by Amber G.
sudarshan wrote:^ I took a look at the continued fractions, very interesting. To instantly intuit a solution on that basis requires one to be directly plugged into the matrix and receiving instant feeds methinks

. What that man could have done if he'd lived longer!
But is there a
formal solution?
Formal solution, as I posted before is:
x = ( (3+2 √ 2)^n - (3 - 2 √ 2)^n) / (4 √ 2)
y = ((3+2 √ 2) ^n + (3 - 2 √ 2) ^n - 2)/ 4
Answers are given by choosing n=0,1,2,3,....
Surprising the "practical" solution is *VERY* easy as 3+2 √ 2 ≈ 5.82842712475 all you have to do is to find (5.82842712475^n) .. for example
y=(5.82842712475^n - 2)/4 (Just take the integer part only

.)
---
In some of the books, I have seen the formula is credited to Euler, but of course, this was well known to Brahmgupta and *many* others for thousands of years.
The method, as you can see, is fairly well known, easy to prove (extremely easy to prove). Interesting this theme does appear many times in competitive exams.
(Similar problem I asked here in brf before - find a right-angle triangle with integer sides (a,b,c) such that b=a+1. (Examples (3,4,5))
-------
Sudarshanji - Just curious, did you find any other solution to my first problem - how high up did you (or your computer program) go? TIA.
Re: BR Maths Corner-1
Posted: 23 Jun 2020 23:41
by Amber G.
sudarshan wrote: <snip>
As an anecdote, a friend of mine, while taking a math course at a US university, had this professor, who introduced the term "Diophantine equations" but said "they are also called Aryabhatta equations, I have no clue why." My friend informed him that Aryabhatta was an Indian mathematician. The wiki entry on Diophantine equations doesn't mention Aryabhatta, but there are other wiki entries (I think the one on Aryabhatta himself) which mention that he preceded Diophantus by 250 years (according to the standard dating - of course there was gross distortion of dates in Indian history during the colonial era). The solution technique he came up with was "kuttaka" (pulverization) - repeatedly reducing the problem to smaller and smaller divisors, maybe that also applies to one specific class of Aryabhatta equations.
Few comments: You and others may like:
-Most (I certainly do) teachers, now give credit to Aryabhatta for first-degree "Diophantine equations". This is of the form Ax + By = C, where A,B and C are integers. His book/documents still survives so we see that this was earliest (as far as I have seen / know) documentation of the method. The method in modern books are also sometimes described as "Euclid" method, Chinese (remainder) theorem etc.. Many old mathematicians (Chinese, Arabs etc) knew/used the method.
- BTW, Aryabhatta was the first to document (to my knowledge).. the other formulas used in my problems - including:
1+2+3+...y -= y(y+1)/2
and 1^2+2^2+3^2 +... x^2 = x(x+1)(2x+1)/6
In his book.
(Also, one of the earliest solution of quadratic equation.
-- Brhamgupta was expert on second degree Diophantine equations ( Ax^2+Bxy+Cy^2+fx+gy+h) type equations. The methods still bears his name although in western books some are credited to Pell and others.
-- Third and higher degrees expert, was Ramnujan.
But to me, joy is discovering many of these equations which can be explained using simple logic.


.
Re: BR Maths Corner-1
Posted: 23 Jun 2020 23:46
by Amber G.
Okay - here is a simple problem (as easy as 1,2,3

) I posed in a group consisting of mainly Google Engineer's
Find three positive rational numbers such that their sum is 6 and the product is 6.
One answer is 1,2,3 as 1+2+3 = 1*2*3 = 6
Any other answer?
(Only fractions - rational numbers which are positives - are allowed.
(Let us see if brfites visiting this forum can find the answer(s) before the other group... computers /books etc are allowed .. googling is discouraged but I can't stop it

)
(Request: Please For this problem (only) _ No invoking great mathematicians

and writing about fantastic theorems ... Just the answer(s) please.. if one answer appears find a different answer - Imagine your audience just know how to add and multiply ordinary fractions! I want to see how many answers we get here in brf ...)
Re: BR Maths Corner-1
Posted: 24 Jun 2020 01:55
by Vayutuvan
sudarshan wrote:Vayutuvan wrote:
In general, there is no general solution method for diophantine equations. That was Hilbert's 10th problem whose statement I am including below. (1)
...
So that means the cubic problem (the harder version of problem 2) also has
no general solution?
No. MRDP theorem doesn't say that. The theorem doesn't say anything about a specific Diophantine Eequation (DE). Examples are many. We already have the two such problems presented by Amber G. ji.
One of the most celebrated (and now solved) DEs is FLT - Fermat's Last Theorem.
What the MRDP theorem states, roughly, is that we cannot know beforehand whether a given diophantine equation has a solution. We would not know it even if we are given as many computational resources - both and space and time - as we demand.
For example, Goldbach's conjecture can be expressed as a system of DEs as follows.
Code: Select all
ap + b(c^2+d^2+e^2+f^2) = 1 ------- (1)
gq + h(k^2+l^2+m^2+n^2) = 1 ------- (2)
p + q = 2x ------- (3)
x > 2 ------- (4)
(1) and (2) say that p and q are prime numbers. We know that every integer can be expressed as the sum of foursquare. It is called the Lagrange's four squares Theorem. What it says is that p and q are primes, i.e. their GCD with any number is 1.
Equation (3) and (4) together say that every even number greater than 4 is a sum of two prime numbers.
We may have to add a few more inequalities of the type (4) to make sure that the problem statement is complete in that encoding I have chosen above.
Similarly, FLT can be encoded similar to the above, and so on. Let us assume that there is a computer that can understand this encoding which means it can understand the problem statement. What MRDP Theorem states is that we cannot program this computer to say whether a DP encoded in this form has a solution or not.
What this means is that every DP has to be solved by one or more 'ad hoc' methods. One doesn't know apriori how complex and how many 'ad hoc' methods are required to show whether even one solution exists, leave alone how many solutions.
Compare this to a system of linear equations in reals. We do have several algorithms of differing complexities to solve a system of linear equations.
I hope I am somewhat clearer now.
Added later: To summarize, Number Theory problems are easy to state as well as easy to understand. On the other hand, they can be arbitrarily hard.
Re: BR Maths Corner-1
Posted: 24 Jun 2020 10:29
by Schmidt
Amber G. wrote:Schmidt wrote:
Same for the similar problem that Amber G gave later
Use a^3 , b^3 ,1 as three terms and AM > GM
Can you expand? (Thanks in advance). (Of course, others can comment too).
--
Background - The problem came to my attention as one niece sent that to me. She is quite bright (her parents, uncles and grandfather include graduates and math professors

) yet was not finding any easy way to solve it. Obviously she (and others) tried AM>GM and other techniques one learns but it came close but not quite. (She could easily prove a^3+b^+1 >=3ab = 3/c or 1/(a^3+b^3+1) <= c/3 but then what? )
(The problem my niece sent was with the terms a^5+b^5+..... The a^3+b^3+1 problem I made it up to show the concept I was trying to teach her using simpler terms).
++++++++++++++++++++++++++
Once your niece got to the step you mentioned ,
Then add all three terms and prove that LHS <= ( a + b + c )/3
All that remains is to prove that ( a + b + c) >= 3
This can be proved by again taking a , b , c together and using AM >GM once more
Re: BR Maths Corner-1
Posted: 24 Jun 2020 11:35
by Amber G.
Schmidt wrote:
Once your niece got to the step you mentioned ,
Then add all three terms and prove that LHS <= ( a + b + c )/3
All that remains is to prove that ( a + b + c) >= 3
This can be proved by again taking a , b , c together and using AM >GM once more
Thanks ,,, but..
Check it again ...If LHS <= (a+b+c) /3
and (a+b+c) >= 3
It DOES NOT mean LHS <= 1

(Just because (a+b+c)/3 is greater than 1 and it is also greater than LHS ==> it does NOT mean LHS is less than 1)
(What you need is a+b+c/3 as less than 1 and that is not the case

)
(Hint: No it is not that easy ... Any other ideas ?

(Thanks in advance -if anyone wants to add )
(As I told you this niece's teachers and parents and all other people were not able to find a good method to solve it - And this niece - who is is in elementary school but can do high-school/college level problems - and her grand-father is a math professor. I do coach some bright kids, hence I sometimes get such questions forwarded to me:) )
Re: BR Maths Corner-1
Posted: 24 Jun 2020 12:38
by Schmidt
You are right
So let me try differently
Since a, b c are positive No's,
We can use a^3 + b^3 >= a^2b + ab^2
Then 1 / ( 1 + acube + bcube ) <= 1 / ( 1 + a square b + absquare )
RHS becomes ABC / ( ABC + asquareb + a square )
Take out ab, you get c/( c + a + b )
Cyclically , original LHS <= ( a + b c )/( a + b + c )
So LHS <= 1