Sudarshanji, Vayutuvanji et all - Okay, I am putting solution to my own problem - Posting the original problem in quotes for convenience, but there is quite a lot of discussion above.
Amber G. wrote:Okay - here is a simple problem (as easy as 1,2,3

) I posed in a group consisting of mainly Google Engineer's
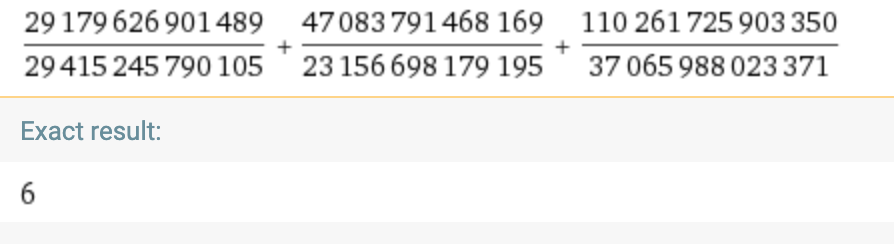
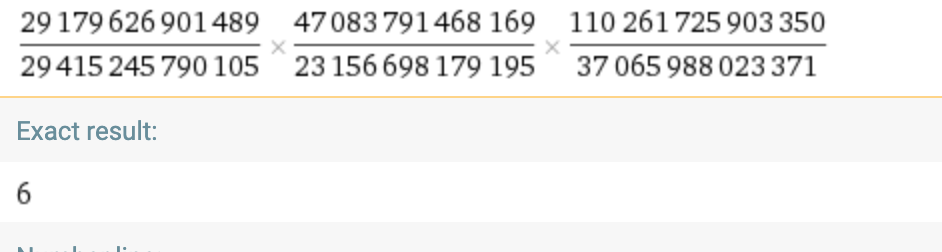
Find three positive rational numbers such that their sum is 6 and the product is 6.
One answer is 1,2,3 as 1+2+3 = 1*2*3 = 6
Any other answer?
(Only fractions - rational numbers which are positives - are allowed.
(Let us see if brfites visiting this forum can find the answer(s) before the other group... computers /books etc are allowed .. googling is discouraged but I can't stop it

)
We got some answers, (by Sudarshanji - see those posts) mostly I think, by trials . This type of problem is less common to be asked in ordinary exams and may be a little harder. Of course there are many resources where one can get more mathematical details and theory but few comments, some may find interesting.
- There are infinite solutions to this problem.. and one can systematically find as many as one want with simple algorithm.
Here is one way - where I just give the method. (As they say this method comes in a dream where Namagiri appears

)
>>>
start with x_0 = 1 and y_0 = 1
Now find the new value of x and y (call it x_1 and y_1) by the method given just below (Method #1 - recursion)
Using these new values of x_1 and y_1, use the same method to find new values of x and y (call it x_2, y_2) .
This way you can get as many values of x and y as you want..
(
for each value, the answer three values would be
6/(3-x) , (6-3x+y)/(3-x) , (6-3x-y)/(3-x)
Since x and y are rational, all three values above will be rational, and you can verify that sum and product of the above three numbers would be 6.
(Sum is easy to see that it is 6, the product, will also be 6, if you follow the method given below to find right x and y)
****
Method #1
calculate m = (17 - y_0)/(7- x_0)
(new) x = m^2 - 7 - x_0
(new) y = m (7- x) - 17
***
That's all, it's that simple.
For example, first set of (x,y) = 1,1
This gives m = (17-1)/(7-1) = 8/3
so new x = 64/9 - 7 - 1 = -8/9
and new y = 109/27
Now when x=1, y=1, (first value) gives the three values 6/2 , 4/2, 2/2 which is (3,2,1)
and the second set gives the values given above.
(6/(3+8/9); (6+8/3+109/27)/(3+8/9) ; (6+8/3+109/27)/(3+8/9)
which is 54/35 ; 49/15; 25/21
Now you can start with (-8/9 and 109/27 as x,y value and get a new set of values..
And repeat...