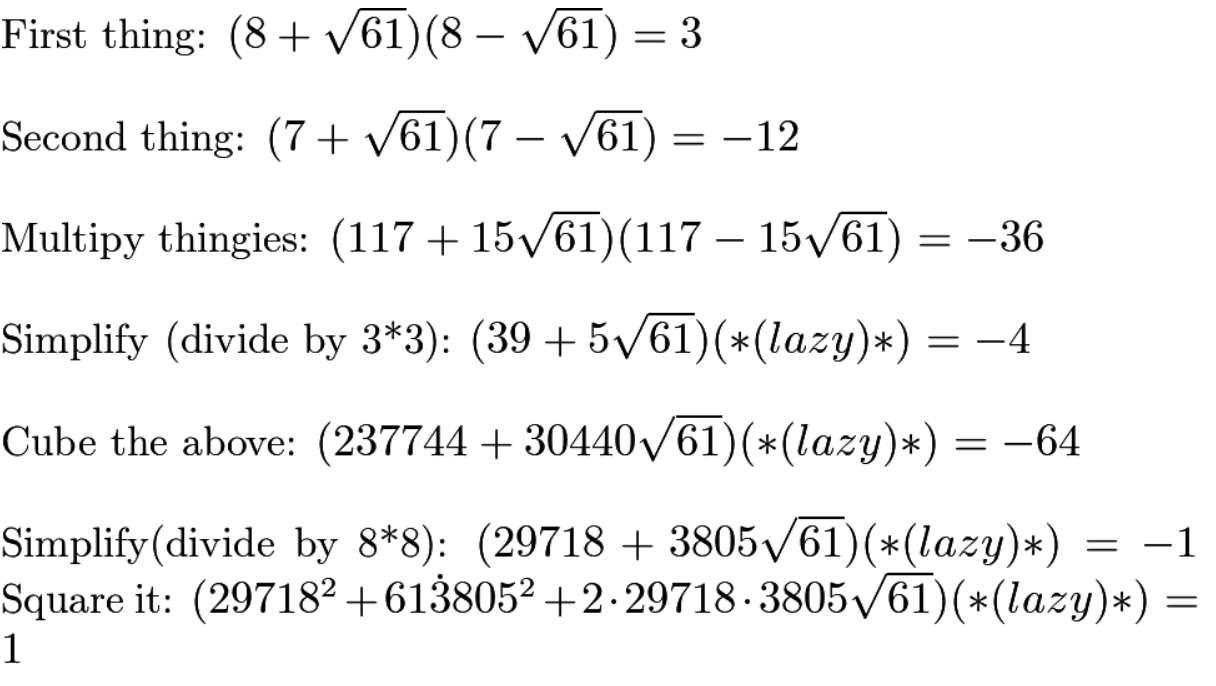Sudarsha et all - (Hope this is useful and inspires some young readers to be interested in math..
sudarshan wrote:I couldn't figure out the Sanskrit text. Why did you pick 8 in the first step, and 7 in the second? Does the text say to do that? I'm guessing because 8 is the smallest number whose square is larger than 61, and 7 is the largest whose square is smaller than 61?
How do you decide when to square/ cube etc.?
I'm asking because I tried with P=2 and P=3 instead of P=61. I couldn't follow the steps like you had above, instead of cubing, I had to square and do some different operations to get 1 on the RHS. Also, the solutions I got for P=2 and P=3 worked, but they were not the lowest possible solutions for either case. For example, for P=2, I got 2*12^2+1=17^2, and for P=3 I got 3*15^2+1=26^2.
But for P=2, the lowest possible solution seems to be 2*2^2+1=3^2, and for P=3, it seems to be 3*4^2+1=7^2.
It's ingenious though. However, one question that I have is - what happens when P is a perfect square? Looking at the equation: P * C^2 + 1 = k^2, one can immediately see that when P is a perfect square, there are no solutions where both C and k are integers (C=0/k=1 doesn't count). How does that work with the above procedure?
The Sanskrit text is very clear and it answers why one picks 8 etc..( when and why to do square/ cube etc might not be clear there - those were my short-cuts)
If Sanskrit is rusty - One can google or see standard math text - the methods are called Brahmgupta's bhavana method ... you can see wiki or for example (
https://bhavana.org.in/the-bhavana-in-mathematics/ (If someone does enough googling - they may find my decades old class notes

- or others work - used for coaching - using modern methods and in simpler terms

)
Bhaskara wrote about this extensively - good text books or wiki - do google on " cakravāla or chakravala (= cyclic) method of Bhaskara" -- This is basically recursive formula - each step (starting with 8^2 ) takes you closer.
Bhaskara gives fairly rigorous treatment - proving how this will work for every number (except perfect square) to give minimal solution in very few steps.
(For those interested - there is *plenty* of literature to see how Bhavana or Chakravala works but basically you start with a number - whose square is as close to 61 - with certain property. .. you work with x^2 - 61 y^2 = k , and keep getting better values of k until you find k=1.
*****
Euler and many others in western world, used continued fraction method - *again* developed by Indian Mathematicians but that work has been translated into English. See my comments about Ramanujan and continued fraction method.
Basically here, one finds continued fraction of sqrt(61) (which is [7+ : 1, 4,3,1,2,2,1,3,4,1,14)].. you do the same computation as Ramanujan did for sqrt(2) ... you get rations like ...7/1, 8/1, 39/5, 125/16, 164/21, 453/58, 1070/137, 1523/195, 5639/722, 24079/3083, 29718/3805, 440131/56353.. etc.. at 22nd term, you will hit the correct answer, and then again 44nd term etc... )
The method is equivalent to Brahmgupta's method but a little slower..
I like my method - posted here in BRF (from a screen of my chat) .. which essentially used only 3-4 steps.


..(First 2 steps are essentially chakravala but "cubing" / squaring etc are my short-cuts not that well known - they save may be dozen or half a dozen steps from pure charavala method)
****
There are *many* fine-points which are very interesting in modern math - basically algebraic fields. Manjul Bhargava (India's first Field Medalist) often talks about Brahmgupta's contribution in his work and credits him.
For us physicists group theory is used in QM and modern physics so this kind of math is quite useful - practically speaking

..
Hope this is all fun and even educational...

..
(For your information, the minimal solution to x^2–9739y^2=1is
2004678915287129865051784235972681465598817784993286048703987347587076305931512617412027372229926151890^2 -
9739*20313634766038988908316803031882483814532877863673358783668788287930891909883492238723036864710413171^2 = 1


)