Bharat Rakshak

^^
Bias is not new to quantitative models. It's the buzz word these days. It is new for data scientists because first time they're venturing into financial services and a lot of creative data is available. If you've worked into US FS sector you would know what to use and what not not to. how to deal with fair lending and compliance.
In cases where you can remove bias you can in others you just cant do that from the technique. The only thing left is to control the data.

UlanBatori wrote:Wow! With Pee Aref and Wikipedia and Google Translator hu needs college? And "AI" can do my thinking 4 me!

On a serious note while building anything mission critical or say building things that directly have a bearing on human life we still see a lot of emphasis on a candidate's education and work history , such considerations are no longer deemed necessary in the internet world where use-case is to build say a dating app, the problem is not only well defined and technically not hard to implement but most importantly you have the luxury of shipping buggy software and simply iterate over it , something which can never be done with mission critical software and ironical as it may sound it pays more to build such stuff .

What is also becoming increasingly apparent is that in the entire ecosystem the need for knowing everything from fundamental building blocks to final application has reduced to only limited set of people who need to do research or say build a solution for an engg. problem . Majority of the monetizeable work out there is at solution/application level and this does not need knowledge of absolute fundamentals it merely requires people to be aware of the lego/building blocks and how they integrate together to orchestrate a story which could solve one or more use cases , hence the 'genuine need' for a college degree is going down , degrees are primarily used only to filter candidates when number of applicants are huge .

ArjunPandit wrote:^^
Bias is not new to quantitative models. It's the buzz word these days. It is new for data scientists because first time they're venturing into financial services and a lot of creative data is available. If you've worked into US FS sector you would know what to use and what not not to. how to deal with fair lending and compliance.
In cases where you can remove bias you can in others you just cant do that from the technique. The only thing left is to control the data.

I have no clue about FS be it US or elsewhere. I have been exposed to bias/fairness issues for autonomous vehicles research.

^^Got it, In FS these things are part of 1 & 3. there are checks in 2, but the key is to avoid direct contact with the enemy. Now FS products can not not be on the spot life threatening so there are luxuries. I am keen to see how they form a part of estimation. Last i checked was using misclassification penalties and metrics as part of 2 itself. remember the more you add in 2 the more data will be required

negi wrote:

UlanBatori wrote:Wow! With Pee Aref and Wikipedia and Google Translator hu needs college? And "AI" can do my thinking 4 me!

On a serious note while building anything mission critical or say building things that directly have a bearing on human life we still see a lot of emphasis on a candidate's education and work history , such considerations are no longer deemed necessary in the internet world where use-case is to build say a dating app, the problem is not only well defined and technically not hard to implement but most importantly you have the luxury of shipping buggy software and simply iterate over it , something which can never be done with mission critical software and ironical as it may sound it pays more to build such stuff .

What is also becoming increasingly apparent is that in the entire ecosystem the need for knowing everything from fundamental building blocks to final application has reduced to only limited set of people who need to do research or say build a solution for an engg. problem . Majority of the monetizeable work out there is at solution/application level and this does not need knowledge of absolute fundamentals it merely requires people to be aware of the lego/building blocks and how they integrate together to orchestrate a story which could solve one or more use cases , hence the 'genuine need' for a college degree is going down , degrees are primarily used only to filter candidates when number of applicants are huge .

theoretically yes, Practically even a dating app would not want to be seen discriminating against latinos and colored folks in matching their dates. Hope you get what I am trying to allude. Of course life threat is a problem of different magnitude. The way it will be handled or is handled currentlyis to pass on low end/maintenance stuff to IT/consults who might be in des and keep the cheddar at home.

Working on beyond visual line of sight (BVLOS) drones, it was just not autonomy of the drone itself but also found major application of AI/ML in operational risk matrix of beyond visual line of sight and that is a system of systems thinking. Involves lot of training data-set from varied sources

Thx. Whether pooch was serious or not, fabulous answers came from it. 99.99% of actually monetizable work is going to be farmed out at fairly low level to people who can do some kind of data analysis/ testing. Reading about Boeing todin will give you a different view of how the "Real World" at the Top does "testing" (only 300-odd Africans/Asians have died so far, so not yet like its a REAL problem..) It will be interesting to see how that evolves: the hyenas are howling all round. Airboos will be particularly thrilled at Stupeed Americaines being the center of attention right now. Waiting to read how it was all due to software outsourced to (u know where).
Another AI problem: Predicting what sorts of disasters to test for, with nonlinear combinations of 127 System of Systems factors acting on each other.

UlanBatori wrote: Another AI problem: Predicting what sorts of disasters to test for, with nonlinear combinations of 127 System of Systems factors acting on each other.

1. Drawing analogy from FS reverse stress testing would be your best guess. I have not crossed the river so thats all i can tell. But in that case you start with what can go wrong and then how does it go wrong! that is one way of testing interconnected systems that i have seen
2. In these cases what can go wrong is not tested individually but also collectively. The art of predicting future is not an easy one. I have seen people keeping things simple work out the best

Apart from Robotics and IOT,

ML is now routine in the the social and consumer space:
like for ads, real time recommendation engines for media consumption, fraud detection, lead generation for sales or other fund generating activities
Russians and others are using it election hacking and other social engineering.

https://www.aitf.org.in/publicopinion
is this a legit govt website? If true, The govt does have a lot to catch up before working on AI

esommuk wrote:https://arxiv.org/pdf/1810.01943

http://sebastianrisi.com/wp-content/upl ... _cig18.pdf
You might have seen this but still this paper brings the questions in more fundamental manner. DARPA is also working on explainable AI.

negi wrote:Fanne sir my two cents ; it's too vast a field , depending on what exactly you wish to accomplish the path you take will vary . Generally speaking if it's say consulting then I would imagine we are not talking about learning the science in itself but actually learning how to identify and classify problems and map them to corresponding models (i.e. application of the technique and not learning the technique in itself), however if you wish to learn the area itself to be able to not just say for solving a problem 'x' you need to apply 'y' framework/technique then you will have to brush up everything right from linear algebra , probability , statistics and even neural networks . Once the method itself is understood learning to program these in python or etc would be the next step.

If it sounds overwhelming what I suggest is this ; identify the area which interests you for example in ITVTY generally speaking the areas where we see ML or it's constructs applied are text parsing/processing (could be NLP) or say media (images/audio/video) if you have an area narrowed down it will make your pursuit more organised and easier to plan for . You can further refine your target area of study if you can reduce it down to an industry problem e.g. customer segmentation , sentiment analysis, general predictive use cases (revenue or churn prediction) or say if it's as simple as extracting text from physical documents (just throwing examples here) . If you have that list you can then find out what would be list of probable models to approximate these problems and then go all the way up the lineage to begin from fundamentals this will keep the scope relatively narrow.

Negi ji and Arjun Pandit Ji,
Maths and I were born for each other, I do some exotic math just as hobby (very niche concerned with my hobby). So ya probability, permutation combo, algebra, calculus, STAT etc. has been my best friend. They do not intimidate me. In fact most of my friend (here at BR and otherwise) have been pushing for me to get into this field.
But I do not really know how to start. A well laid out course and lucid material going to appropriate depth goes a long way. Perhaps that is 80% of the fight, 20% is the drive and effort to know it. I am seeking help on the 80% of it.
From my IIT preparation day, it was good to know what book to read for each chapter/area for Physics/Math/chemistry. Once you knew it, it was easy. Many were lost trying to study things from the wrong place (and could have been very successful) had they known the right place. I would not do it just for consulting, but to know and maybe be a successful entrepreneur (hint: What is hot or going to be hot). From Business application I don't have any passion, I can swing any way.

fanne wrote: Negi ji and Arjun Pandit Ji,
Maths and I were born for each other, I do some exotic math just as hobby (very niche concerned with my hobby). So ya probability, permutation combo, algebra, calculus, STAT etc. has been my best friend. They do not intimidate me. In fact most of my friend (here at BR and otherwise) have been pushing for me to get into this field.
But I do not really know how to start. A well laid out course and lucid material going to appropriate depth goes a long way. Perhaps that is 80% of the fight, 20% is the drive and effort to know it. I am seeking help on the 80% of it.
From my IIT preparation day, it was good to know what book to read for each chapter/area for Physics/Math/chemistry. Once you knew it, it was easy. Many were lost trying to study things from the wrong place (and could have been very successful) had they known the right place. I would not do it just for consulting, but to know and maybe be a successful entrepreneur (hint: What is hot or going to be hot). From Business application I don't have any passion, I can swing any way.

Here is a list that might help:
Linear Algebra
Vectors
definition, scalars, addition, scalar multiplication, inner product(dot product), vector projection, cosine similarity, orthogonal vectors, normal and orthonormal vectors, vector norm, vector space, linear combination, linear span, linear independence, basis vectors
Matrices
definition, addition, transpose, scalar multiplication, matrix multiplication, matrix multiplication properties, hadamard product, functions, linear transformation, determinant, identity matrix, invertible matrix and inverse, rank, trace, popular type of matrices- symmetric, diagonal, orthogonal, orthonormal, positive definite matrix
Eigenvalues & eigenvectors
concept, intuition, significance, how to find
Principle component analysis
concept, properties, applications
Singular value decomposition
concept, properties, applications
Calculus
Functions
Scalar derivative
definition, intuition, common rules of differentiation, chain rule, partial derivatives
Gradient
concept, intuition, properties, directional derivative
Vector and matrix calculus
how to find derivative of {scalar-valued, vector-valued} function wrt a {scalar, vector} -> four combinations- Jacobian
Gradient algorithms
local/global maxima and minima, saddle point, convex functions, gradient descent algorithms- batch, mini-batch, stochastic, their performance comparison
Probability
Basic rules and axioms
events, sample space, frequentist approach, dependent and independent events, conditional probability
Random variables- continuous and discrete, expectation, variance, distributions- joint and conditional
Bayes’ Theorem, MAP, MLE
Popular distributions- binomial, bernoulli, poisson, exponential, gaussian
Conjugate priors
Miscellaneous
Information theory- entropy, cross-entropy, KL divergence, mutual information
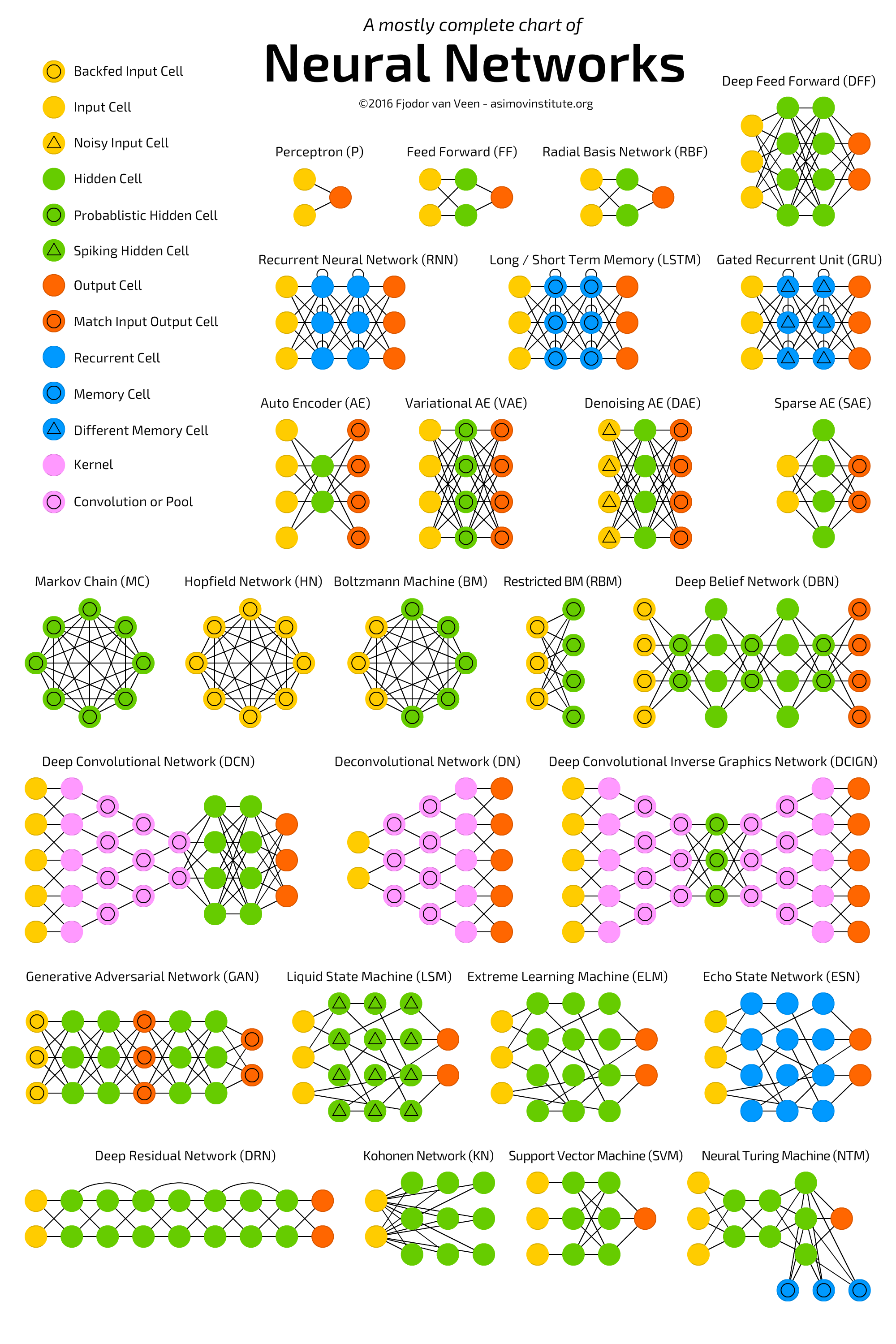
Markov Chain- definition, transition matrix, stationarity

Further, an understanding of open source frameworks ( building blocks/implementation of above mathematical concepts ) ,some programming chops to get hands dirty to mess with data and visualize the results ,ability to use tools hosted on cloud hosted infrastructure , broad system / system of systems level big picture understanding of the problem , availability of pertinent data are the requirements.
Mastery is all this is not possible for an individual so a team with complimentary skill sets really help drive AI projects.

Dang! Natural intelligence doesn't require one to learn all that, why the artificial variety I wonder.

UlanBatori wrote:Dang! Natural intelligence doesn't require one to learn all that, why the artificial variety I wonder.

.. because it's "artificial".. process of building natural intelligence starts with conjugal bliss

fanneji,
really good to hear from a negative chaiwallah. if you are comfortable with maths, then this field should be cake walk for you. what you need to know is what you want to know. If your aims are entreprenuail then look in a reverse manner. Application ->Field->data/technique. Unfortunately, we all are blind men holding tusk, tail and legs of the elephant and each of us will have their viewpoints.

So is there an AI for Kindergartners that I can view, please? It CAN'T be that difficult...
Oh well.. first teach them to type "Art-e-fissal Intel-e-gentz Kindergarten" in Google.

This article ain'g got none
So we learn on Day 1 of our schooling that articles written by ppl who "program robots" have not much useful knowledge.

OK!!!! AI Textbook for Pre-Schoolers! THAT's my level. Ooops! Its in Chinese!

AI education initiative launched this July by the China Education Technology Association Smart Learning Committee and UNESCO. The aim is to democratize AI education in 100 Chinese schools, introduce pre-teens to the basics, strengthen teenagers’ capability for using intelligent and applied technologies, and help train hundreds of new AI teachers.

cloud-based AI e-learning platform that students can access via PC or WeChat. The platform supports major machine learning frameworks including TensorFlow, CNTK, and Caffe; programming environments Scratch 3.0 and Python Integrated Development Environment (IDE); and includes digital copies of the 33 AI textbooks and a broad scope of use cases. Platform development was reportedly led by Google AI experts in Beijing.

OK, I am **NOT** going to kindergarten in China.

In April 40 high schools in Shanghai began using Fundamentals of Artificial Intelligence, a nine-chapter AI textbook compiled by SenseTime, the world’s most valuable AI startup. Two months later, Suzhou University published its Primary and Secondary School Artificial intelligence Series.

“With the rise of automation, new skills are emerging as valuable in the age of AI and are often not the focus of K-12 education. These include problem finding, inquiry, flexibility, collaboration, creativity, systems thinking and technological literacy to name the basics,” says Simsarian. “AI changes what we teach the next generation starting in Kindergarten because the next generation will have jobs that do not exist yet.”

OK, now that v r learning in kindergarten that PYTHON is not a gentle slow-moving creature that loves to hug people, but a vicious Programming Environment from which, once entered, few ever emerge, may I please have a PYTHON code that I can use to start training a robot?

And here it is (I guess):

Mars in distributed version is now available on Linux and Mac OS. Click this link for the Mars Github page.

In terms of time-sink that is more powerful than the Galactic Black Hole. I guess we won't be seeing many of the postors on this thread for a while..

I knew it! Posting real work will (a) drive away the non-serious and (b) make the Serious disappear because they will be trying to get the code to compile.

UlanBatori wrote:I knew it! Posting real work will (a) drive away the non-serious and (b) make the Serious disappear because they will be trying to get the code to compile.

https://github.com/search?q=tensor

There are 35000 tensor repos in Github and 15794 written in Python along with boatload of tutorials.
Python doesn't need "compiling" or may be Ulan Bator has come up it's version of language that needs compiling.

Good night

UlanBatori wrote:I knew it! Posting real work will (a) drive away the non-serious and (b) make the Serious disappear because they will be trying to get the code to compile.

Picking -e-nit . Python is an interpreted language .

All in good humor onlee . Bliss to naat utarofy my chaddi. Humble muj onlee

That Mars tensor framework (https://github.com/mars-project/mars ) comes way down the ladder in terms of usage and acceptance compared to tensorflow,keras & pytorch.

Alibaba has just started playing same playbook that Google tried during early days of Tensorflow i.e release half baked framework and then ask others to test and debug ( guinea pigs ).

That would be Guinea PIGS (Poor Indian Graduate Student)?
In Ulan Bator we would not know difference between "Interpreter" and "Compiler". We hit "run", whatever happens happens. Fate.

I was hoping the Kindergarten Courses would explain terms such as "tensor", "Keras" etc. Why does AI need such huge computing? Surely not to simulate the thought processes of HUMANS? Like say, Dar ka Butt?

Machine Learning Fairness

https://hackernoon.com/learning-ai-if-y ... f0002c9b32

https://towardsdatascience.com/the-most ... b6f2367464

Based on my limited experience with this field in industry (yet to go through the India's AI policy), but still
1. There's a lot of old wine in new bottle. People are overselling a lot of stuff that used to pass as analytics in past
2. the maturity of many areas, esp text/NLP etc is not yet there in financial services as compared to IT giants like google/fb, even though these companies have tonnes of data
3. many of the things are just leveraging robotics and that is being passed through
Net net a lot of repackaging going on. The real juicy stuff or as we say noise-signal ratio in the output is low, just as its there for a fad.
My hunch is that its real percolation & large implications are at least half a decade away.
However the luxruries are clearly getting commoditized and in next 10-15 years it will meet teh same fate as IT

https://yourstory.com/2019/04/startups- ... e-learning

Delighted to see some work being done here...during one of my searches

http://www.cse.iitd.ernet.in/~mausam/

https://tech.economictimes.indiatimes.c ... h/66870633

havent gone through these links will post the details tonight from them..but if you folks read in between please share your insights

Deleted by See Eye Aay

If there is unique voter ID (Aadhar) and web access, why can't there be web-based voting with AI etc used as needed to ensure accuracy? No lines, no booth-capturing, HUGE reduction in poll expense and security issues. What are the problems with this? Answer may be very useful.

UlanBatori wrote:If there is unique voter ID (Aadhar) and web access, why can't there be web-based voting with AI etc used as needed to ensure accuracy? No lines, no booth-capturing, HUGE reduction in poll expense and security issues. What are the problems with this? Answer may be very useful.

hahaha, I had thought about it...but then there's a lot of fun in that,
1. imagine poootin and eleven deciding sitting in urals or say wuhan
2. xiaomi/lenovo/oppo/vevo/ and what not downloading data of our voting
3. Dr Zola type of congi character identifying based on fb posts, or my twitter posts why I hate fundoos and congoons so much, and then delhi police "knocking on heaven's door" like they did for Baba ramdev
4. how's gerry mandering gonna happen
5. What role does our own mookes bhai have based on the voting info or fb posts, i guess he'll be neutral coz he's always in power
6. Last but not the least some forever single guy sitting in iit lab hacking just for fun or releasing my voting data publicly
7. Oh yes and my fav, abdool casting vote for all 4 suckeenas at home itself. Or engineers voting after unable to watch pawn after n8tyumrika has been banned by IBM (IB Ministry)
the list can go on. My point being the leverage of a single event is tremendous. Of course I am aware these things are under actively pursued in Yakland, and all 5 above points are baby yakdung

UlanBatori wrote:If there is unique voter ID (Aadhar) and web access, why can't there be web-based voting with AI etc used as needed to ensure accuracy? No lines, no booth-capturing, HUGE reduction in poll expense and security issues. What are the problems with this? Answer may be very useful.

Do away with voting. Use AI to predict declare who wins.

In voting there are 5 issues:
1. Ensure that one votes IFF (If and only If) one is a registered voter. In the right constituency.

2. Ensure that no one can see who one votes for.

3. Ensure that the vote that one intended to cast is indeed the vote that was cast.

4. Ensure that the vote that one ended up casting is indeed the vote that ends up being counted.

5. Ensure that the actual vote count is what is announced.

#1 is easy. Aadhar only identifies you as a voter. Only 1 vote allowed per Aadhar. Aadhar is supposed to be updated to remove dead people, foreigners etc. When an Aadhar vote is registered the owner is informed that s(he) has voted, just like credit card transactions today.
#2: There has to be some randomizer that then guards the entrance to the "polling booth" where your vote is cast and (ha ha! ) no one can tell who is voting. This is not any worse than the security issues of BlockChain, hain? (not that I know how that is done). So there is no trace from voting preference to voter. You are not seen going to the polling booth, and in whose car/bus. There is no "black mark" on your ungli to identify you to the Mujaheddin as someone who did not boycott the evil yindoo election. Rain or shine, as long as there is electricity and Net connection you can vote.

#3 is the Miami Dade County 2000 election problem: they made sure that the huge polling sheet was confusing enough that many ppl of limited attention span voted wrong.

#4 is the EVM fraud: aka Gujranwala Problem where Mushy got 142.394 % of the registered voters to vote for him. Heads rolled for that when the percentage was revealed.

#5 is an ED problem. Putin may send entire ED to Krasnoyarsk via Vladivostok on foot in January and Xi may send his ED to accompany them via Mongolia, but I think India has surmounted that.

Take BRF Poll Thread. Can you tell that I am one of the 6 who voted for RaGa, hain? Oops! OK, I can try explaining that I did it just to see how many would do that, but the Holy Polis may nevertheless tell me like after Guj2002 festivities that

The Blessed Bhamasura Will Put Da Hex On U.

Of course the randomizer can be infiltrated I suppose. That is another BlockChain type problem, I am sure there are solutions.
Verifying #3 is the credit card payment problem. If that is secure, why not voting? It is actually MUCH better in the peace and security of your own computer than on a strange screen in Miami polling booth.
Verifying #4 may require innovation. How do you do that with no one seeing WHO cast the vote?
What would be the "paper trail" that satisfies the voter, the different candidates and the ED that all is well?

NRaoji's point is interesting. AI should be able to predict, for instance, that I am a strong RaGa/MahaGaddha-Bandar fan based on my fB and BRF postings. 400% accurate. I could post bumper stickers saying

VOTE Hammer-Sickle-Star
(its easier than thinking)

and everyone will know I worship Comrade Pinnarayi Yakdungwali

UB ji,

Techs really roll down the steppes. Scientists Create Speech From Brain Signals

Looks like there is a Yak herder from your peachy muluk. IP is yours.

Anyways, no need for internet or any Aadhar. Plug into the mind and ur done!! One has to only think of their Aadhar number and vote mentally. They just need to make sure that they are not dreaming of a Stormy of Karen when they "vote", else you will have the wrong person leading India.

Anyways, best to you. Have fun.

I saw an estimate on this thread that there are over half a million desis engaged in AI work? That is a big payroll, isn't it? Is that coding? Data collection? Trying to get a handle on the present. Distribution over industries?
Voter site may require visual scan of Aadhar. But the bigger use of AI is in getting 1 step ahead of any scammers.