Bharat Rakshak

^^Congratulations to the USA team for their achievements at the International Mathematical Olympiad! 4 golds and 2 silvers, including Luke Robitaille, who ranked 3rd overall.
Congratulations to the India team - 1 Gold (Pranjal Srivastava), 1 Silver and 3 Bronze.


(In 2019 Pranjal became the youngest Indian to win gold - And as I mentioned then, he won again.)


(Meanwhile Pakistan distinguished itself by coming in the last - Four 0's and two 1's making a total of 2 total points)

I am very glad and proud for Pranjal getting a gold again!

I posted about Pranjal in BRF 3 years back in 2018! predicting his bright future !

Here are my post(s) from 2019 and 2018 ..

Amber G. wrote:FYI: Pranjal got Silver last year, and at that time I was impressed with him. He is getting gold this time! (It is not official - we may have to wait for as much a day .. - but I am quite sure, seeing the partial results). He has two more years to represent India.

I posted this last year:

Amber G. wrote:^^^ For the record ( Name, score (out of 42) and Medal) (*** This is year 2018 **)
IND1 Sutanay Bhattacharya 21 Bronze
IND2 Spandan Ghosh 21 Bronze
IND3 Amit Kumar Malik 10 HM
IND4 Anant Mudgal} 26 Silver
IND5 Pulkit Sinha 26 Silver
IND6 Pranjal Srivastava 28 Silver
(I am specially impressed by Pranjal - He is youngest - had 4 perfect scores (Prob 3 and Prob 6 were missed) - and method used were nice).. I am sure he is going to do very well in the next olympiad and math in general.

***
Prob 3, (which I posted above) turned out to be rather difficult. None of Indian team solved it. Only 2 from USA did it.
I was kind of surprised as I posted above, when I checked, the problem has indeed came in Scientific American. (This is probably 30-40 years late, but I knew how to solve it then ..)

Problem is posted above. (With the hint that solution is in SA one can do internet search)..
(Hint: Answer, is one can not find a solution for N>5 (so not solution for 2018))

One solution posted in SA came from 4th grader (for N=6)indeed quite simple.

Allow me to cross-post another Olympic News here:
About 2021 International Math Olympiad which just concluded.
India's Pranjal Srivastava Bags Gold Medal At International Mathematical Olympiad 2021
I predicted Pranjal's bright future 3 years back here in BRF. see my cross post in In this post in Math Thread

Just today I was reading an article related to mathematics and came across a reference to this book and the ted talk by the author Daina Taimina, a Latvian mathematician.

https://smile.amazon.com/Crocheting-Adv ... 367375079/

Okay, once again here is a problem to try - A well known famous problem which stumped a very famous Fields Medalist but later has appeared in a few contests.... and it looks extremely easy.

If a and b are non-negative integers and also:

(a^2+b^2)/(ab+1) = k is an integer,
prove that k is a perfect square.

Amber G. wrote:Okay, once again here is a problem to try - A well known famous problem which stumped a very famous Fields Medalist but later has appeared in a few contests.... and it looks extremely easy.

I got part of the solution (I used Excel again and 1 sheet of paper). I can rattle off sets of numbers which will fulfill the conditions. I'm just not able to prove that these are the only numbers, ergo, that k can only be a perfect square.

For [a, b, k], ordered such that a < b, I can prove that k cannot be greater than a^2. Also, that k = a^2 will always work. Also, that a cannot be equal to b, except when a = b = 1.

Here are number triples for [a, b, k] which satisfy the conditions:

[1, 1, 1]
[2, 8, 4]
[3, 27, 9]
(In general - [a = m, b = m^3, k = m^2], m going from 1 to infinity)

But also:

[8, 30, 4]
[27, 240, 9]
[64, 1020, 16]
(In general - [a = m^3, b = m^5 - m, k = m^2], m going from 2 to infinity)

Should I post the solution I have so far, or give others a chance?

sudarshan wrote: ...
I got part of the solution
Here are number triples for [a, b, k] which satisfy the conditions:

[1, 1, 1]
[2, 8, 4]
[3, 27, 9]
(In general - [a = m, b = m^3, k = m^2], m going from 1 to infinity)

But also:

[8, 30, 4]
[27, 240, 9]
[64, 1020, 16]
(In general - [a = m^3, b = m^5 - m, k = m^2], m going from 2 to infinity)

Should I post the solution I have so far, or give others a chance?

Nice.
I think it may be okay to discuss it here .. but let us give a few days to others ... The problem is *very* famous and has appeared in JEE and such exams (originally it came from a math olympiad). There is a beautiful theme to solve such problems. Easy way is to ask an "old fashioned" math professor but it might be fun to try it without that.

Amber G. wrote: Nice.
I think it may be okay to discuss it here .. but let us give a few days to others ... The problem is *very* famous and has appeared in JEE and such exams (originally it came from a math olympiad). There is a beautiful theme to solve such problems. Easy way is to ask an "old fashioned" math professor but it might be fun to try it without that.

There is a recurrence relation. For any (perfect square) k larger than 1, there are an infinite number of solutions for [a, b].

For example:

k=1 (this one is trivial, the interesting cases come for larger k)

[a, b] = [0, 1], [1, 1], [1, 1], [1, 1], .... (same solution keeps repeating)

k=4

[a, b] = [0, 2], [2, 8], [8, 30], [30, 112], [112, 418], [418, 1560], ....

k=9

[a, b] = [0, 3], [3, 27], [27, 240], [240, 2133], [2133, 18957], ....

k=16

[a, b] = [0, 4], [4, 64], [64, 1020], [1020, 16256], [16256, 259076], ....

k=25
.
.
.
.

I think I'm tantalizingly close, I can see the pattern and a hint as to why k can't be anything but a perfect square, but can't quite get there. I was originally generating the above from a rather complicated mathematical recurrence relation, but once I got a few pairs, it became clear that the pattern could even be calculated by hand (with some difficulty).

Will wait to see what others come up with.

Nice.

but once I got a few pairs, it became clear that the pattern could even be calculated by hand

Virahṅka and Hemacandra (12 th centruy ) talks about such pattern and Naryana Paita (14th century) too...
Essentially if you know x1 and x2 then x3 = k*x2 - x1..


(so if k=4 then you start with 2,8

get 8*4 - 2 = 30
30*4 - 8 = 112
112*4 - 30 = 418
418*4 - 112 ....
The series is 2,8,30,112,418... and any two neighbors will do. ..

---
(how to prove that *only* square k will give such patterns..)
(There are some beautiful anecdotes with this problem and some really elegant ways .. more later)

This is such a beautiful problem. On the face of it quite simple, but very hard in practice. A solution would be appreciated

Tanaji wrote: This is such a beautiful problem. On the face of it quite simple, but very hard in practice. A solution would be appreciated

Yes, I agree. For solution see link in this message and also see below.).

This problem is very famous, quite old (30+ years old when it first appeared in IMO) and the method to do such problems is (now) taught in most problem books.. as said this or very similar problems have appeared in JEE and such exams. (Problem is also famous because one of worlds best mathematician (who was a young boy then) failed to solve it that exam.

I was discussing this recently and have discovered a *really* neat geometrical proof - requires elementary school basic and have another elementary proof - which I will post.

Meanwhile those, who want to see the solution, for this problem and the general method, here is a one link. This particular problem is solved here.

I will post my solution in a separate post.

Amber G. wrote:The problem is *very* famous and has appeared in JEE and such exams (originally it came from a math olympiad). There is a beautiful theme to solve such problems.

Not fair. Really. Does JEE test what the test takers know or what they don't? These kinds of "trick" problems were the staple of Mathematical Tripose. If somebody solves it, does it mean that one can do research in math? Conversely, if one fails to solve that one is relegated to doing I-Banking bhoosa?!!!

Tanaji wrote: This is such a beautiful problem. On the face of it quite simple, but very hard in practice. A solution would be appreciated

As I said before, NT is full of "simple" looking problems which are impossible to solve. I think it is even possible to write a program to generate those problems. Start from a specific solution and generate a generic problem. I conjecture that all such generated problems are AS (almost surely - a measure-theoretic concept) hard to solve.

Tanaji wrote: This is such a beautiful problem. On the face of it quite simple, but very hard in practice. A solution would be appreciated

Inverse problems are hard to solve. RSA depends on that property. One unsolved conjecture in Cryptography is "Are there true one-way functions?".

Since NT is amenable to such formulations, it is the favorite of cryptographers who are in search of a true one-way function.

sudarshan wrote:..I think I'm tantalizingly close, I can see the pattern and a hint as to why k can't be anything but a perfect square, but can't quite get there.

Yes. Here is one * extremely * easy way. (Hope people enjoy it - My method which I have used with students - I have not seen this method in other places )

The basic concept, most of us learned in the third grade math - elementary division - (quotient remainder concept. Eg if you divide 30 by 8 you get 3 and 6 remainder. The key point is remainder is less than divisor.

(This is same as writing 30/8 as 3+6/8 . Of course, one can also write it as 4 - 2/8. - remainder - (in this case is -2 and (absolute value =2 ) is still less than 8 )

Rest is simple!! ( But continue reading further if need be )

Here are basic steps:
-- If b=0 then k = a^2 and nothing more to prove.
-- if a=b only solution is a=b=1 and k=1 ( which is very easy to prove)

so assume a>b>0
now k = (a^2+b^2 ) / (ab+1)
write it as (by dividing both numerator and denominator by (ab)
k = ((a/b)+ (b/a)) (1+ 1/(ab))
So easy to intuitively see that k is quite close a/b ,( both b/a and 1/ab are smaller than 1)
in fact (k-a/b ) = (a^2+b^2)/(ab+1) - a/b
= (a^2*b + b^3 -a^2*b -a)/(b(ab+1)) = b^2/(ab+1) - a/(ab^2+b)
Since a>b, obviously both terms on right are less than 1 so difference (absolute value) is less than 1
(b^2/(ab+1) < b^2/(ab) < b/a and second term is less than 1/b^2)

So one can write a = kb + c where |c| < b (This is how division works, remainder is less) ( c can be negative but its absolute value is less than b). (We have proved that difference between k and a/b is less than 1)

Substituting this in k = (a^2+b^2)/(ab+1) and canceling out some terms we see
k = (b^2+c^2) / ((b(-c) + 1)..
So if (a,b) works as a solution ==> I found a solution (b,c) where c is less than b..

I can continue this getting a smaller and smaller c .. eventually it has to reach to zero, and in that case the k would be a perfect square).( A moment's though tells you that k is not only a perfect square, it is GCM of (a and b))

____
If the method, needs some clarification one example can make it clear:

if we know k=4 and a=112 and b=30 works (check out it works because (111^2+30^2)/(112*30+1) is indeed 4)
The divide 112 by 30, get quotient 4 and write 112/30 = 4 - 8/30
Now 30/8 .. write it as 4*8 - 2/8
Now write 8/4 = 2 + 0
(One sees that 112,30 works ==> 30,8 works ==> 8,2 works ==> 2,0 works ..)
So no matter how high you start, if you find a solution .. you can always find a smaller solution for that k till you reach one number a zero)
QED
---
These methods introduces two very important and fun concepts - used in many math problems (and I teach to students)
1 - Standard methods of finding another set of integer roots if one set is known - (Very helpful in cryptography etc)
2 - Fermat Infinite Descent ( similar to Induction) method in Math.

Okay here is a simple looking problem, perhaps first originated from a Kerala Mathematician in the 15th Century - perhaps not as easy as it looks but still fun..

1 - 1/4 + 1/7 - 1/10 + 1/13 - .....

(Fair to consult any book you like, fair to use computers, fair to use any advance math tool or take help from any math professor you know but see if we can find an answer..)

Hint: Easy to see the answer is positive, less than 1 and greater than 3/4 (and less than 25/28).

Amber G. wrote:Okay here is a simple looking problem, perhaps first originated from a Kerala Mathematician in the 15th Century - perhaps not as easy as it looks but still fun..

1 - 1/4 + 1/7 - 1/10 + 1/13 - .....

(Fair to consult any book you like, fair to use computers, fair to use any advance math tool or take help from any math professor you know but see if we can find an answer..)

Hint: Easy to see the answer is positive, less than 1 and greater than 3/4 (and less than 25/28).

If you plug it in here:

https://byjus.com/infinite-series-calculator/

with the series definition being:

Sum { ((-1)^n)*(1/(3*n+1)) } where n goes from 0 to infinity, you get an answer as:

PI/(3*sqrt(3)) + log(2)/3

The log is of course a natural logarithm.

The series also looks very similar to the Madhava series for the arctangent of 1 (with a sum of PI/4). That series is:

1 - 1/3 + 1/5 - 1/7 + 1/9 - ...

So the denominators increase by 2 each term in the above series:

Sum { ((-1)^n)*(1/(2*n+1)) } where n goes from 0 to infinity

Whereas with the series you have, the denominators increase by 3 each term.

Interestingly, the sum of the series you have, comes out to be close to (but not quite) Sin(1) (1 - of course being in radians). So it is close to (but somewhat - about 0.7% - less than) the sine of the angle subtended by the arc of a circle, whose length is the radius of the circle.

You said - "take help from any math professor you know" - so can I take help from you?

sudarshan wrote:
The series also looks very similar to the Madhava series for the arctangent of 1 (with a sum of PI/4). That series is:

1 - 1/3 + 1/5 - 1/7 + 1/9 - ...

Yes, Madhava of Sangamagrama (Kerala) is the great mathematician I was thinking of and the problem was inspired by this beautiful Madhava's series..!
Wiki (https://en.wikipedia.org/wiki/Madhava_of_Sangamagrama covers his life, including this series nicely.

Note that this was done a few centuries before Newton and Leibniz (or Gregory). Now mathematicians call it Madhava (instead of Gregory or Leibniz series).

Essentially if you start with geometric series, say 1+x+x^2+ ... where x is less than 1, it can be summed as 1/(1+x).

So 1/(1+x^2) = 1 - x^2 + x^4 - x^6 + ...
If you integrate each term, you get:
Arctan(x) = x - x^3/3 + x^5/5 - x^7/7 + ...
(which results into famous series, as you mentioned, when you put x = 1 as:
π/4 = 1 - 1/3 + 1/5 - 1/7...

___
The above problem, I chose 1/(1+x^3) instead of routine x^2.. The integral is little harder but it is still beautiful. ..
(Thanks for https://byjus.com/infinite-series-calculator/ link.. in return, the integral can also be done here ... The result matches your value.

that visual representation is irrelevant, no?!

Amber G. wrote: Essentially if you start with geometric series, say 1+x+x^2+ ... where x is less than 1, it can be summed as 1/(1+x).

So 1/(1+x^2) = 1 - x^2 + x^4 - x^6 + ...
If you integrate each term, you get:
Arctan(x) = x - x^3/3 + x^5/5 - x^7/7 + ...
(which results into famous series, as you mentioned, when you put x = 1 as:
π/4 = 1 - 1/3 + 1/5 - 1/7...

___
The above problem, I chose 1/(1+x^3) instead of routine x^2.. The integral is little harder but it is still beautiful.

Oh, so that's how it's done. But how did Madhava come up with his series representations of sine, cosine, arctangent, etc.? Was he aware of the Taylor series (using the currently accepted term) expansion for 1/(1+x^2)? And also that the integral of that would be the arctangent?

The problem with these series are that they are slow to converge. So evaluating PI to 6 decimal places would need at least a million terms, more like 10 or 100 million in practice. 8 decimal places would need 100 million to 10 billion terms. It goes as the inverse of the required precision (since each term in the series is the inverse of a linearly-growing denominator).

Vayutuvan wrote:that visual representation is irrelevant, no?!

No. Visual representation and connection between area of a curve and integrals is important aspect - Historically Integral calculus was developed before differential calculus. Anyway the cut-and-paste came directly from mathematical app .

sudarshan wrote:

Amber G. wrote: Essentially if you start with geometric series, say 1+x+x^2+ ... where x is less than 1, it can be summed as 1/(1+x).

So 1/(1+x^2) = 1 - x^2 + x^4 - x^6 + ...
If you integrate each term, you get:
Arctan(x) = x - x^3/3 + x^5/5 - x^7/7 + ...
(which results into famous series, as you mentioned, when you put x = 1 as:
π/4 = 1 - 1/3 + 1/5 - 1/7...

___
The above problem, I chose 1/(1+x^3) instead of routine x^2.. The integral is little harder but it is still beautiful.

Oh, so that's how it's done. But how did Madhava come up with his series representations of sine, cosine, arctangent, etc.? Was he aware of the Taylor series (using the currently accepted term) expansion for 1/(1+x^2)? And also that the integral of that would be the arctangent?

His books (many of which were written by his students later on - but still centuries before Newton) writes the series of sine, cos and many other functions..almost with similar methods .. beauty of simple expansion of 1/(1+x^2) and thus getting the arctan series is quite impressive. (Even now many math books do not use this simple and intuitive method to teach)...

BTW historically there is little doubt that his work was available to Leibniz and some other Western mathematicians ..Kerala school's textbooks were transmitted to Europe via Jesuit missionaries and traders who were active around the ancient port of Muziris at the time.. and had quite bit of influence on later European developments in analysis and calculus. ("Study of infinite series, calculus, trigonometry" etc). Famous book Mahajyānayana prakāra (written in Malyalam in 16th century ) cites Madhava as the original source for these formulas and gives proofs for the expansion of such infinite series.

(Value of pi - accurate up some 15 digits were routinely present in these books using his methods)

The problem with these series are that they are slow to converge. So evaluating PI to 6 decimal places would need at least a million terms, more like 10 or 100 million in practice. 8 decimal places would need 100 million to 10 billion terms. It goes as the inverse of the required precision (since each term in the series is the inverse of a linearly-growing denominator).

This is true, but actually math provided by him - and techniques on how to make them much more convergent for ease of calculation - is still *very* helpful. "Saddle point Method" of Euler - Maclaurin way to "transform" such slow convergent series - somewhat standard methods now .

For example, as you say you need a billion or so terms to get to 8-9 digits of accuracy.. but a slight modification, as Madha says and used was to use:

arctan(1) = arctan(1/2)+arctan(1/3).. Now if you use, 30 terms of each series, you will get 10-15 places of accuracy...

One of my *first* use of computer (this was way back in 60's with IIT Kanpur's IBM 7044) I got value of pi for a few *hundred* places of decimals - using this well known Madhava's trick..

pi/4 = 4 arctan(1/5) - arctan (1/239)

pi = 16 (1/5 - 1/(3*5^3) + 1/(5*5^5) - 1/(7*5^7) + ....) - 4 (1/239 - 1/(3*239^3)+ ...)

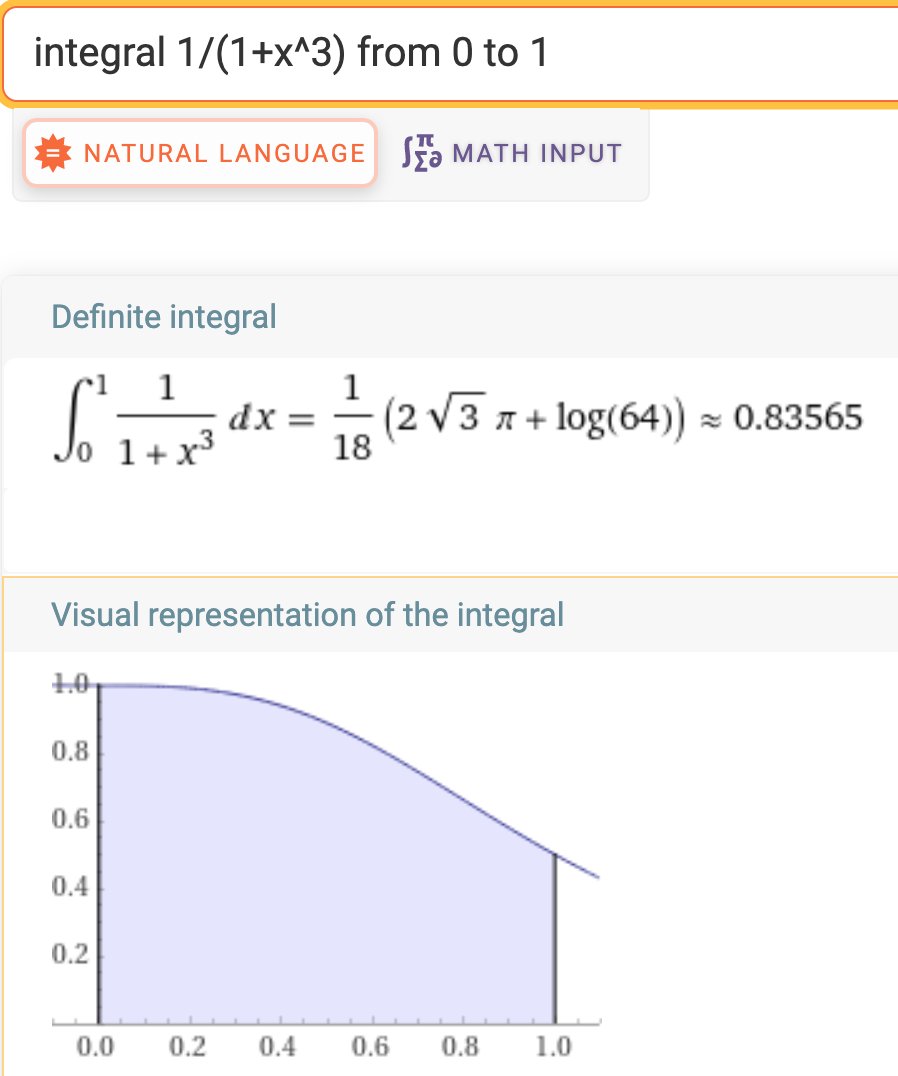
Amber G. wrote:.. but a slight modification, as Madha says and used was to use:

arctan(1) = arctan(1/2)+arctan(1/3).. Now if you use, 30 terms of each series, you will get 10-15 places of accuracy...

Now that's ingenious! I'm impressed. I read that Madhava (or his disciples) actually quoted the value of PI to 18 places in one of their works, and I was wondering how many decades of work that represented, calculating it with that slow series. As you say, the modification above will yield a much faster converging series.

But what kind of procedure would allow somebody to identify that atan(1/2) + atan(1/3) was the same as atan(1)? Or, as you say below, 4*atan(1/5)-atan(1/239)?

One of my *first* use of computer (this was way back in 60's with IIT Kanpur's IBM 7044) I got value of pi for a few *hundred* places of decimals - using this well known Madhava's trick..

pi/4 = 4 arctan(1/5) - arctan (1/239)

pi = 16 (1/5 - 1/(3*5^3) + 1/(5*5^5) - 1/(7*5^7) + ....) - 4 (1/239 - 1/(3*239^3)+ ...)

Ingenious again, and definitely very fast-converging, but same question as above - how was this identity determined?

What datatype did you use with that computer? Float only gives 8 places of accuracy, double gives about 16. I'm guessing you implemented some kind of string-based representation of the numbers, with long division to go from one term in the series to the next?

Actually, a question that I had was - is there any practical use to knowing the value of PI to billions of places (I believe that's the current status)? I don't believe it's used in cryptography. If one takes the known radius of the observable universe, and if one wants to calculate the circumference down to the diameter of a hydrogen atom, the number of decimal places of PI that one needs, is - 39! If one now wants to calculate that circumference down to 1 Planck length (I believe this is the limit of discretization of space itself) - the number of digits necessary is - 63. If one instead wants to compute the volume of the known universe down to the volume of every last hydrogen atom, that would need PI down to 117 decimal places.

Is it just an academic exercise, knowing the value of PI to "billions of digits" accuracy?

Also, when people claim that the "Greeks knew the value of PI to great accuracy" - that is such a bare-faced lie. The Greek numbering system was the precursor of the Roman one, so it represented numbers by letters in the same way, except that four would be represented as IIII (or four of the equivalent Greek letter) rather than IV (subtract 1 from 5) in the Roman system. So there is no such thing as "decimal places" in this numbering system. The concept of "decimal places" comes from India, and in fact it is impossible to represent any number (let alone PI) to any number of decimal places using the Greek numbering system.

In fact, the Greek number system doesn't even permit multiplication or division the way we know it, so even 22/7 isn't useful - if one had a circle of radius (say) 11 and a quarter cubits, and one wanted the circumference - doing the multiplication of (11 1/4) by 22, and then the division of that by 7 - well, go ahead and try it with the Roman number system (basically the same as the Greek one).

So far as I can gather, what the Greeks actually had, was a geometrical procedure for approximating the circumference of a circle of known radius. The compass and ruler construction procedures for bisecting angles, generating 60 degree angles, etc. that we learned in school, seem to have come from the Greeks. And they came up with that, because they had no good way to multiply or divide with their numbering system. So what they did was to construct a 60 degree angle, then bisect it a number of times, and do that in such a way that they could approximate the circumference of a circle by a regular polygon with 96 sides. Then they would take the perimeter of that polygon as the length they needed for their architectural projects involving circles.

One can represent the circumference of a circle by regular polygons, and get approximate values for PI that way. For example, as below:

No. of sides--------Approx. value of PI
----------------------Inscribed polygon-----------------Outer polygon--------------------Average

3----------------------2.598076211----------------------5.196152423----------------------3.897114317
4----------------------2.828427125----------------------4------------------------------------3.414213562
5----------------------2.938926261----------------------3.63271264-----------------------3.285819451
6----------------------3------------------------------------3.464101615----------------------3.232050808
10---------------------3.090169944----------------------3.249196962----------------------3.169683453
12---------------------3.105828541----------------------3.215390309----------------------3.160609425
24---------------------3.132628613----------------------3.159659942----------------------3.146144278
48---------------------3.139350203----------------------3.146086215----------------------3.142718209
96---------------------3.141031951----------------------3.1427146-------------------------3.141873275
192--------------------3.141452472----------------------3.14187305-----------------------3.141662761

So even with a regular polygon of 96 or 192 sides, one barely gets a value of PI more accurate than 2 to 4 decimal places, and one might as well go with 22/7.

EDIT:

Seems like even taking the average PI value from the inscribed and the outer polygon doesn't help that much.

END EDIT

So the next time somebody claims that the "Greeks knew the value of PI to great accuracy," one should ask the claimant to write down the value of PI to the claimed accuracy, using the Greek or Roman number system.

Amber G. wrote: BTW historically there is little doubt that his work was available to Leibniz and some other Western mathematicians ..Kerala school's textbooks were transmitted to Europe via Jesuit missionaries and traders who were active around the ancient port of Muziris at the time.. and had quite bit of influence on later European developments in analysis and calculus. ("Study of infinite series, calculus, trigonometry" etc). Famous book Mahajyānayana prakāra (written in Malyalam in 16th century ) cites Madhava as the original source for these formulas and gives proofs for the expansion of such infinite series.

I think those Jesuits also copied a lot of astronomical data from India (literally copied - as in - wrote it down word for word and number for number) and took it to Europe, and this was the data which drove the "Gregorian" calendar reform. From what I read, the decision in Europe was to have an extra day every four years, because they thought the European public would not be comfortable with a fractional number of days in a year. Whereas in India (at least Kerala/ TN, which still follow solar calendars, as opposed to the luni-solar one in the rest of India), the year was defined as 365.25 days (fractional - i.e., if the year started at 6:00 AM one year, then the next year would start at 12:00 PM on the 366th day). Not sure how true this last bit is. But this would mean that the current solar calendar that the world follows, is actually a step back (sophistication-wise) from what was extant in S. India at least as far back as the 1500's.

Some parts of the world still follow the older Julian calendar. Like Russia and Ethiopia. So Christmas in both these countries (they're both Xtian majority) comes in January. This is one of the bonds that Ethiopia shares with Russia, another bond of course being Alexander Pushkin, one of whose great-grandfathers was Ethiopian (I think he was "gifted" to Peter the Great). They still proudly teach Pushkin's poetry in Ethiopian schools, as an Ethiopian friend told me.

Ciprian prize (2022) is to be awarded to Professor Nikhil Srivastava and his colleagues for solving a 50 year old problem. Nikhil earlier won the George Polya Prize in 2014, and the Held prize in 2021.50-Year-Old Math Problem. Congratulations.
Nikhil Srivastava Helps Solve a Famous 1959 Problem

Some may be interested in this great event - Prof. Manjul Bhargava, Prof Ken Ono and director Matt Brown about Ramanujan! Prof. Steven Strogatz is the host for "Starring Math". Pre-registration required. It is scheduled on Dec 20. (see details below)

For those who do not know, Prof Bhargava - the first Indian American to win Fields (= Math Nobel), and Prof Ono are world renowned number theorists. They were also the technical adviser for the great Ramanujan movie - "The Man Who Knew Infinity". The event is sponsored by National Museum of Mathematics.

For details see: <see MoMath's website >
The event is likely to be filled quite fast - registration is required - there may be fee for non-members.

Amber G. wrote:Ciprian prize (2022) is to be awarded to Professor Nikhil Srivastava and his colleagues for solving a 50 year old problem. Nikhil earlier won the George Polya Prize in 2014, and the Held prize in 2021.50-Year-Old Math Problem. Congratulations.
Nikhil Srivastava Helps Solve a Famous 1959 Problem

I posted about Kadison-Singer conjecture and the solution by Marcus, Speilman, Srivastava IIRC. It is a very interesting proof because it used Computational Mathematics.

Spielman, Marcus and Srivastava suspected that the answer was yes, and their intuition did not just stem from their previous work on network sparsification. They also ran millions of simulations without finding any counterexamples. “A lot of our stuff was led by experimentation,” Marcus said. “Twenty years ago, the three of us sitting in the same room would not have solved this problem.”

Speilman got the Nevalinna prize by then for what is called Support Graph Theory, Smoothed Analysis (which was used to show why Simplex Algorithm, even though exponential in the worst case - on pathological problems explicitly constructed to show that Simplex Algorithm visits all vertices of a polytope, does well on most Linear Programming problems which arise in applications, and one more result (I forget).

Gil Kalai gave the lecture at IMC, Hyderabad where Daniel Speilman was presented with Nevanlinna Prize. I will try to find a link and post it here.

Amber G. wrote:

Vayutuvan wrote:that visual representation is irrelevant, no?!

No. Visual representation and connection between area of a curve and integrals is important aspect - Historically Integral calculus was developed before differential calculus. Anyway the cut-and-paste came directly from mathematical app .

Yes, Integral Calculus came before Diff. Calculus due to the need to "measure" something.

Indian mathematician Neena Gupta wins Ramanujan Prize 2021 for her work in algebraic geometry

https://indianexpress.com/article/educa ... d-7673906/

Lisa wrote:Indian mathematician Neena Gupta wins Ramanujan Prize 2021 for her work in algebraic geometry

https://indianexpress.com/article/educa ... d-7673906/

This is great news .. As such an young age, she is the third women ever to receive this honor. She is the second Indian woman after Sujata Ramadorai -- only other Indian woman with this honor.

Today is also Ramanujan's Birthday - India's PM declared it a National Mathematics Day - celebrated as an important event.

As posted few posts above - I hope some people attended it.

Amber G. wrote:Some may be interested in this great event - Prof. Manjul Bhargava, Prof Ken Ono and director Matt Brown about Ramanujan! Prof. Steven Strogatz is the host for "Starring Math". Pre-registration required. It is scheduled on Dec 20. (see details below)

For those who do not know, Prof Bhargava - the first Indian American to win Fields (= Math Nobel), and Prof Ono are world renowned number theorists. They were also the technical adviser for the great Ramanujan movie - "The Man Who Knew Infinity". The event is sponsored by National Museum of Mathematics.

For details see: <see MoMath's website >
The event is likely to be filled quite fast - registration is required - there may be fee for non-members.

I highly recommend the movie - "The man who knew Infinity" - everyone talks about it and people see it again and again.

Here is a treat for those who are seriously interested in math and art From Mathematics Museum - it's about 1 hour long but enjoyable - about the movie, about math by Prof Ken Ono - the renowned mathematician who helped with the direction of the movie to make it great.
https://youtu.be/Qvoou69SNGI
****
Ken Ono, Manjul Bhargava were speakers in this year's event too.
***
Here is an easy (relatively speaking ) math problem to honor the Mathematics Day and Ramanujan..
a and b are natural numbers (positive integers).. find all values of a and b such that:
(a^(2^b) + b^(2^a)+11) is divisible by (2^a + 2^b)

I think those Jesuits also copied a lot of astronomical data from India (literally copied - as in - wrote it down word for word and number for number)

..
There is no doubt, actually it is fairly well documented.
Gauss (One of the greatest mathematician) who has seen and commented on the work of people like Bhaskara, once estimated that some of the parameters (calculated about 2000 or 1000 years ago) calculated by these Indian mathematicians were possible only if these mathematicians had access to accurate data from previous 500 years or so -- Means people like Bhaskara had access to accurate astronomical data for centuries before them.

^^^ Just to show just one sample - 1,400 years ago, Mahabhaskariya of Bhaskara wrote this approximation for the sine function (0 ≤ x ≤ π). He actually credits this to his ancient books -- so the formula may have been discovered about 500 years before he wrote about it.

The formula - written in modern math language - (I am writing it, translation from original written in modern math notation using degrees)

sin(x) = 4(180-x)x/(40500 - (180-x)x)

Just try to see how accurate this is -
Here is the graph from 0 to 180 degrees - Its absolutely accurate for 0, 30, 90, 150, 180 degrees and for the rest the difference is *very* small - I have drawn the error magnified 10 times! - still it is negligible.

On this National Mathematics Day in India.. allow me to post a very special photo - In front of Ramanujan's home is Prof Ono and late prof Dick Askey (who led the fundraising effort that gave Ramanujan's widow the statue of Ramanujan ( bust made by Paul Granlund).

(With all the honors bestowed upon Ramanujan - his widow Janaki remained poor and mostly ignored by India (and it's government) supporting herself by teaching tailoring and running a tailoring shop - In 1962 some of the Indian scientists celebrated 75th anniversary and powers to be decided to have a bust made of Ramanujan to honor him - but nothing much came out of it - Prof Askey (and many Indian and world mathematicians) then led an effort to raise money to make the statue - there was pension established for Ramanujan's widow..When APJ was president more was done - MMS when he was PM - made Dec 22 'National Mathematics Day' -- The present GoI is very supportive of mathematics and science in general)

Just for fun:

Can you find non-trivial (iow x>1) integer solutions for x such that:
1^2+2^2+3^2+4^2 +..... x^2 is a perfect square.

https://dlmf.nist.gov/

This is a great resource for special functions and software for computing these functions. It has 36 chapters.

Foreword
Preface
Mathematical Introduction
1Algebraic and Analytic Methods
2Asymptotic Approximations
3Numerical Methods
4Elementary Functions
5Gamma Function
6Exponential, Logarithmic, Sine, and Cosine Integrals
7Error Functions, Dawson’s and Fresnel Integrals
8Incomplete Gamma and Related Functions
9Airy and Related Functions
10Bessel Functions
11Struve and Related Functions
12Parabolic Cylinder Functions
13Confluent Hypergeometric Functions
14Legendre and Related Functions
15Hypergeometric Function
16Generalized Hypergeometric Functions & Meijer G-Function
17q-Hypergeometric and Related Functions
18Orthogonal Polynomials
19Elliptic Integrals
20Theta Functions
21Multidimensional Theta Functions
22Jacobian Elliptic Functions
23Weierstrass Elliptic and Modular Functions
24Bernoulli and Euler Polynomials
25Zeta and Related Functions
26Combinatorial Analysis
27Functions of Number Theory
28Mathieu Functions and Hill’s Equation
29Lamé Functions
30Spheroidal Wave Functions
31Heun Functions
32Painlevé Transcendents
33Coulomb Functions
343j, 6j, 9j Symbols
35Functions of Matrix Argument
36Integrals with Coalescing Saddles
Bibliography
Index
Notations
List of Figures
List of Tables
Software
Errata

Amber G. wrote:Just for fun:

Can you find non-trivial (iow x>1) integer solutions for x such that:
1^2+2^2+3^2+4^2 +..... x^2 is a perfect square.

With summation of series and then writing a quick shell script - I got x=24.

^^^Nice!.
x=24 is the only (apart from x=0,1) answer.

This is a famous/classic problem - conjectured by Lucas in 19th century but not proven till 1918 - using elliptical functions and complicated math. Some less complicated methods to prove this came later.

Found a very easy method to prove that x=24 is the only answer - using only elementary number theory. So this may be a good challenging problem for those who like math.

https://en.wikipedia.org/wiki/Cannonball_problem

The above puzzle is the Cannonball problem

Find n and y both integers such that 6y^2 = n(n+1)(2n+1)

One elementary proof is here. https://www.jstor.org/stable/2323911 which can be read if you register. You can read 100 articles/month online for free if you register.

On Ramanujan's birthday I posted:

Amber G. wrote:
I highly recommend the movie - "The man who knew Infinity" - everyone talks about it and people see it again and again.

Here is a treat for those who are seriously interested in math and art From Mathematics Museum - it's about 1 hour long but enjoyable - about the movie, about math by Prof Ken Ono - the renowned mathematician who helped with the direction of the movie to make it great.
https://youtu.be/Qvoou69SNGI
****
Ken Ono, Manjul Bhargava were speakers in this year's event too.
***
Here is an easy (relatively speaking ) math problem to honor the Mathematics Day and Ramanujan..
a and b are natural numbers (positive integers).. find all values of a and b such that:
(a^(2^b) + b^(2^a)+11) is divisible by (2^a + 2^b)

Here is an ad featuring Ken Ono. -- Enjoy .. (This may be shown at Super Bowl!)