Bharat Rakshak

Amber G, I'm not related to any Prof Satapathy AFAIK, there seem to be several. But who knows... I recently was made aware of some longish relation we had to late Sri PVNR from my father's side and VVGiri from my mother's side so... There seems to be a cosmic conspiracy to make me feel infinitesimally insignificant !

Thank you. My nephew may know this group, he is an iitk alumini

IMHO, he should cast the net wider including MSR India, Bangalore (where Ravi Kannan works and Katyal IIRC), IIITH, TIFR at Pune University (where Karmarkar is - joint with NIC) and a few other places including private research labs (if any). If he is not wedded to working in the academia, his options are wide open. Especially in the chip industry. SAT Solvers are used extensively in the verification and circuit minimization in digital systems. Ciruit minimization helps in reducing the gate count for implementing a given boolean function. This reduces the size and hence better utilization of the real estate. Another application area I forgot to mention is AI (learning of boolean formulae, Automatic Theorem Proving/Proof Assistants, ML). It is possible he wants to crack the holy grail of computer science; resolve the P =? NP question. But lower bounds seem to be a dead end for resolving this question. But one never knows.

If he comes with a separation theorem for NP and CoNP, then the immediate consequence is P != NP.

Cyrano wrote:Mouli Sr (lol reminds me of a poem from Sumathi shatakamu) - heads the labs now, he is my BiL

Well since it's anyway in public domain
https://www.drdo.gov.in/labs-establishm ... atory-drdl

He did his ME from ECE, OU. He might be a student of my BiL Dr. Yoganadam Yeleshwarapu, or my professor Dr. DC Reddy.

Thank you Yayutuvan garu, I'll share your suggestions with him.

Cyrano wrote:Thank you. My nephew may know this group, he is an iitk alumini

Best wishes.. (some how I was pretty sure he was an iitk alum).

Meanwhile here is something you (or your nephew and others) may enjoy: Dr Somenath Bisbas writeup about that fantastic discovery in 2002
Story of a Discovery

Beautifully written article ! I need to read it a few more times to get more of it

^^^ Thanks. Glad you liked it. If you look in this dhaga around 2002 .. I put several posts about this before the news started appearing in Indian News papers.

-- Tidbit - US India's relationship was not that good then and US hesitated not give a visa to Prof Agrawal though many universities were inviting him here.. with lot of pressure from US academics, he did come to US but Nitin and Neerj (his students) were not able to make the US tour... These guys now have gotten many honors/awards from India now.

--- One interesting part about this work (which is similar to the paper you posted of your nephew) is math part is not that hard to understand even for those who are not expert in the field -- this is quite rare so it is enjoyable.

Amber ji,
Shared that article with my nephew, here is what he wrote back:

Thanks! It was a great read, definitely an amazing story of a ground-breaking discovery.

I took Manindra’s undergraduate algebra class when I was at IITK. The final proof of their result is so simple that it was included as an assignment for us! Luckily I still had it in my cloud storage, I’m attaching it, I’m sure you will find it interesting.

If anyone is interested in taking a crack at the assignment please share your email in some creative form and I'll send it to you.

https://scottaaronson.blog/?p=304

Ten Signs a Claimed Mathematical Breakthrough is Wrong

Yesterday several people asked my opinion of a preprint claiming to solve the Graph Isomorphism problem in deterministic polynomial time. I responded:

If I read all such papers, then I wouldn’t have time for anything else. It’s an interesting question how you decide whether a given paper crosses the plausibility threshold or not. For me personally, the AKS “PRIMES in P” paper somehow crossed it whereas this one somehow doesn’t.

Of course, I’d welcome an opinion from anyone who’s actually read the paper.
...

Rest of the blog post is very interesting. Scott Aronson got his PhD under Umesh Vazirani who got his PhD under Manuel Blum. Impagliazzo got his PhD from Manuel Blum also, as I said before.

There is a similar blog post for sciences which I will link to in Physics dhaga.

Cyrano wrote:Amber ji,
Shared that article with my nephew, here is what he wrote back:


If anyone is interested in taking a crack at the assignment please share your email in some creative form and I'll send it to you.

Please, if you can, post it here.
I am glad he enjoyed the article.
---
As said, that particular idea is quite elegant - and very rare that work could be understood (and thus enjoyed) by people who are not that expert in the field.

Yuri Manin has died. He was a noted mathematician who has influenced numerous fields of math and physics and was a nice human being.

Please, if you can, post it here.

AmberG,
Its a copy disabled pdf, it may be a © issue as well to post it here. .

*deleted*

Yes I did, will reply tomorrow am from my pc

thanks for the pdf.

The final proof of their result is so simple that it was included as an assignment for us! Luckily I still had it in my cloud storage, I’m attaching it, I’m sure you will find it interesting.

Yep! This is indeed in the problem set (for undergraduates). and that too in CS and not pure mnt ...but then Neeraj and Nitin were undergraduates too. Hats off to IITK's computer science dept.

Most of the places in India, at least when I was there -- very little math is taught in Engineering (even less in Medical schools) or even in Science departments. I learned abstract algebra (due to knowing some great mathematicians in my circle) earlier but it wasn't until graduate school when this was taught in IIT Kanpur (and that too, I took graduate courses in Math department). I am glad that now a lot of it is covered in undergraduate courses.

Okay here is a fun problem for 2023. Enjoy:


A rectangular cuboid (a box) has a body diagonal (longest diagonal joining the opposite corners) measuring 2023.
Also, all sides are integers. In addition at least two face diagonals are integers too.
Can you find solution(s) (or prove that there are none)!

***
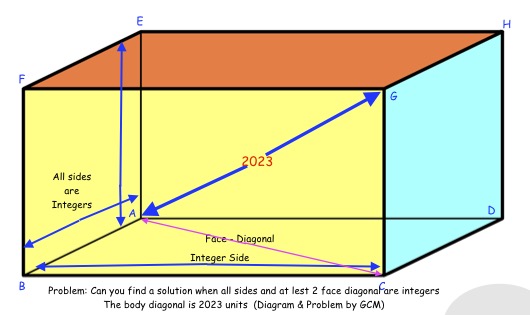
Note: The problem is from a similar problem by I saw on social media --
(The problem is not very hard - but not exactly sure how hard or easy it is for this audience )
You can use calculators, computers, math-packages etc if you like, but *none* are needed. Just some basic number theory (and perhaps blessings from Brahmgupta) is all you will need in addition to paper and pen
(Cyrano you may like to ask this to your nephew - with tools available to him it is a very simple problem)

If the main diagonal is 2023 (an odd number), and all the sides are integers, then:

1. either one side is an odd integer, and the remaining two are even

or

2. all three sides are odd integers

For case 2. - if all three sides are odd integers, and if two face diagonals are also integers, then these two face diagonals have to both be even integers. So for each face, we have Pythagorean triplets, which can be represented as:

(a,b,c) where a and b are odd, and c is even.

This cannot be a primitive triplet, because primitive Pythagorean triplets cannot have c (hypotenuse) being even. So, the GCD of (a, b, c) has to be greater than 1. But this GCD also has to be odd (otherwise it won't divide a or b). Also, (A=a/GCD, B=b/GCD, C=c/GCD) will be a primitive Pythagorean triplet, in which C=c/GCD has to be even (since c is even, and GCD is odd). This again leads to a primitive Pythagorean triplet:

(A, B, C) with even C. Which is impossible.

So case 2. is impossible.

Still working on case 1. But just by brute force Excel, case 1 also seems impossible.

Still working on case 1. But just by brute force Excel, case 1 also seems impossible.

^^^ Important clarification:
"Two face diagonals" here means, two diagonals on the *same* face (which are equal in anycase). (IOW if one can find all sides integers, and one diagonal integer, another diagonal is automatically an integer."

(One can prove that it is impossible to have two diagonals on different faces as integer when the body diagonal is 2023)

BTW - The problem when *all* sides, and all diagonals and all body diagonals are integers in a general case is still *unsolved* -- nobody has found an example of such a box (and nobody has proved that it is not possible)...

Amber G. wrote: BTW - The problem when *all* sides, and all diagonals and all body diagonals are integers in a general case is still *unsolved* -- nobody has found an example of such a box (and nobody has proved that it is not possible)...

Do you mean a general hexahedron (not a cuboid) by that highlighted phrase?

^^^ I meant cuboid (a box - whose all faces are rectangles).

Amber G. wrote:

Still working on case 1. But just by brute force Excel, case 1 also seems impossible.

^^^ Important clarification:
"Two face diagonals" here means, two diagonals on the *same* face (which are equal in anycase). (IOW if one can find all sides integers, and one diagonal integer, another diagonal is automatically an integer."

(One can prove that it is impossible to have two diagonals on different faces as integer when the body diagonal is 2023)

BTW - The problem when *all* sides, and all diagonals and all body diagonals are integers in a general case is still *unsolved* -- nobody has found an example of such a box (and nobody has proved that it is not possible)...

Examples of 3 integer sides with one face diagonal being integer and body diagonal = 2023
273,952,1764
448.840,1785
756,1617,952
840,952,1575
1008,1127,1344
1071,952,1428

10 lines of python and 10 min runtime w/o parallel processing.
No examples of two face diagonals being integers.

It would be challenging to do this without the code i.e. just logical/mathematical reasoning.

Amber G. wrote: ^^^ Important clarification:
"Two face diagonals" here means, two diagonals on the *same* face (which are equal in anycase). (IOW if one can find all sides integers, and one diagonal integer, another diagonal is automatically an integer."

Oh in zat caze zere are zo many zoloozions...

(a,b,c) being the three sides:

a---------------------b-------------------------c-------------------Face diagonal------------------Main diagonal
952------------------273----------------------1764---------------1785-----------------------------2023
952------------------756----------------------1617---------------1785-----------------------------2023
952------------------840----------------------1575---------------1785-----------------------------2023
952------------------1071---------------------1428---------------1785-----------------------------2023
1785-----------------448----------------------840-----------------952------------------------------2023
1127-----------------1008---------------------1344---------------1680-----------------------------2023

EDIT: posts crossed, but I think you can do it analytically, with the theory of primitive and non-primitive Pythagorean triplets.

As a hint - the prime factors of 2023 are 7, 17, 17 (this also comes from the previous post by Amber G - (2+0+2+3)(2^2+0^2+2^2+3^2)^2=2023).

Use the prime factors to find the primitive triplets, then scale those up until the main diagonal comes to 2023.

For example: (8,15,17) scaled up by 7 X 17 gives (952,1785,2023), now split 1785 similarly to get 4 primitive triplets, etc.

Primitive triplets are ALWAYS of the form: (m^2-n^2, 2mn, m^2+n^2) with m and n being an odd/ even or even/ odd pair.

Will try to post a more rigorous solution soon.

Great! Sudarshan , & Skumar, yes there are these six solutions..

skumar wrote:
Examples of 3 integer sides with one face diagonal being integer and body diagonal = 2023
273,952,1764
448.840,1785
756,1617,952
840,952,1575
1008,1127,1344
1071,952,1428

10 lines of python and 10 min runtime w/o parallel processing.
No examples of two face diagonals being integers.

Also:

It would be challenging to do this without the code i.e. just logical/mathematical reasoning.

and

but I think you can do it analytically, with the theory of primitive and non-primitive Pythagorean triplets.

As a hint - the prime factors of 2023 are 7, 17, 17 (this also comes from the previous post by Amber G - (2+0+2+3)(2^2+0^2+2^2+3^2)^2=2023

Use the prime factors to find the primitive triplets, then scale those up until the main diagonal comes to 2023.

For example: (8,15,17) scaled up by 7 X 17 gives (952,1785,2023), now split 1785 similarly to get 4 primitive triplets, etc.

Sudarshanji - Yes that was the theme ... similar lines are using Gaussian primes or using primes in more general sense.. (as we were talking about Manindra's method etc)..

So allow me to post the solution: Which is very simple It is same as what Sudarshanji was hinting at but uses simple arithmetic , Enjoy:
*****

All it involves is factoring into Gaussian primes.


Our system consist of "numbers" a+ib where
i = sqrt(-1). All ordinary integers are in the "system " (b=0) and the system is closed under addition and multiplication.

Then c^2 =a^2+b^2 can be "factored" into (a+ib)(a-ib) so all one needs is to factor in this system!

Here all the odd ordinary primes of the form (4k+3) are also Gaussian primes. but *all* (4k+1) type of primes are *not* Gaussian primes. eg 7 is prime in this number system but 5 = (2+i)(2-i) and 17 = (4+i)(4-i) can be factored.
(This is a famous result of number theory - Thanks to Brahmgupta )

With this - it is super easy... if you can factor .. eg 2023 = 7*17^2
(Only primes of the type 4k+1 need to be paid special attention and factored further)

***
Let sides be (a,b,c) and diagonal be d
we have a²+d²=2023²
and b²+c²=d²
Now 2023=7*17²
7 is Gaussian prime but 17 is not.
17=(4+i)(4−i)
17²=(4+i)²(4−i)²=(15+8i)(15−8i)
17⁴=(15+8i)²(15−8i)²=(161+240i)(161−240i)
So there are only two solutions for a²+d²=2023²
2023²=(7⋅17⋅15)²+(7⋅17⋅8)²
and 2023² = (7⋅161)²+(7⋅240)²

So possible values of d are:
Case 1 d = 7*17*15 = 7*3*(4+i)(4-i)(2+i)(2-i)
Case 2 d =7*8*17 = 7*8*(4+i)(4-i)
Case 3 d = 7*161 = 7*7*23 (all Gaussian primes)
Case 4 d= 7*240 = 7*16*3*(2+i)(2-i).

Case 3 will generate no solutions.
Case 2 when d = 7*8*17 gives b = (7*8*15) c = 7*8*8 as (4+i)^2 = (15+8i)
Case 4 will give d = 7*16*3*5 gives b=7*16*3*3, c= 7*16*2*4 as (2+i)^2 = (3+4i))
Case 1 gives 4 solutions (how you combine the prime factors
or d = 21*5*17 gives (b,c) as (21*5*15, 21*5*8 ) or (21*17*3 ,21*17*4)
or (21*77, 21*36) or (21*84,21*13)

(as (4+i)(2+i) = 7+6i and (4+i)(2-i) = 9+2i)
and (7+6i)^2 = (13+84i) and (9+2i)^2 = (77+36i)

(Brahmgupta's Blessings makes it easy !

Didn't know about Gaussian primes before, but golly, they look interesting. I guess Pythagoras' theorem applies to their study, because the modulus of a complex number is essentially the hypotenuse of the right triangle with the real and imaginary parts as the other two sides?

From what I understood, just like primes can't be factored in integer arithmetic, Gaussian primes cannot be factored even in the domain of (integer-arithmetic) imaginary numbers.

It's interesting, because the square of an odd integer will always be 1 modulo 4, never 3 modulo 4. Which is why I guess integers of the form 4k+1 are not Gaussian primes, whereas those of the form 4k+3 are.

So is the number 15 a Gaussian prime, or not? It can be factored in integer arithmetic as 3 * 5, but not in the complex integer arithmetic you indicated (it is of the form 4k+3)?

EDIT: Amber ji, I got the answer, re-reading the earlier post - 15 is not a Gaussian prime, since a Gaussian prime is a REGULAR PRIME of form 4k+3.

ASIDE: since we're talking about Gaussian primes, integers of the form 4k+1, 4k+3, etc. - a simple trick for getting the remainder of any integer, upon division by 4. Let's take a long number:

7582950732103932491

Is this a Gaussian prime, or not? I.e., is it of the form 4k+3, or 4k+1?

What is it's remainder upon division by 4? It is the same as the remainder of the last two digits (91) upon division by 4, which is, 3. This will always work, because 100 is divisible by 4. In this particular case, we are dealing with:

75829507321039324 * 100 + 91, but the first term is guaranteed to be divisible by 4, because 100 is divisible. So one only needs to look at the last two digits.

If you want the remainder upon division by 8, just look at the last 3 digits (1000 is divisible by 8 ); by 16 - last 4 digits (10,000 is divisible by 16) and so on.

(In the same way, most people can tell an odd number from an even one, just by looking at the last digit, since 10 is divisible by 2).

This leads to a follow-on question - is the above number a perfect square? It can't be, because the square of an odd integer can never be 3 modulo 4. One can eliminate half of all numbers as perfect squares this way, just by looking at the last two digits, because the square of an even number will also be always 0 modulo 4, never 2 modulo 4.

On top of this, the square of any number ending in "5" will always end in "25." So any number ending in "05," "15," etc. simply can't be a perfect square.

273

448 - a little after Fa Hian

840
952
1008
1071

1127 - leading up to Slave dynasty (1206 - 1290)

1344 - Tughlaq dynasty (1321 - 1413)

1428 - Sayyid dynasty (1414 - 1451)

1575 - https://en.wikipedia.org/wiki/1575
March 3 – Battle of Tukaroi: The Mughal Empire decisively defeats the Karrani dynasty of Bengal

1617 - https://en.wikipedia.org/wiki/1617
September 1 – The weighing ceremony of Jahangir is described by the first English ambassador to the Mughal court, Sir Thomas Roe
September 3 – Birth of Roshanara Begum, Mughal princess (d. 1671)

1764 - https://en.wikipedia.org/wiki/1764
October 22 – Battle of Buxar: The British East India Company defeats the combined armies of Mir Qasim, the Nawab of Bengal, the Nawab of Awadh, and Mughal Emperor Shah Alam II.

1785 - https://en.wikipedia.org/wiki/1785
January 27 – The University of Georgia in the United States is chartered by the Georgia General Assembly meeting in Savannah. The first students are admitted in Athens, Georgia in 1801
February 9 – Sir Warren Hastings, who has been governing India on behalf of King George III as the Governor-General of the Presidency of Fort William (later British India), resigns. Sir John Macpherson administers British India until General Charles Cornwallis arrives 19 months later

2023 - Let's make some positive history!

Amber G. wrote: So allow me to post the solution: Which is very simple It is same as what Sudarshanji was hinting at but uses simple arithmetic , Enjoy:
*****
....

Enjoyed this but it is and it is not "simple arithmetic"

^^^ Wow..
FWIW two comments:
- A odd perfect square is not only 4k+1 type but also has to be 8k+1. (Eg xxx021 can not be a perfect square).
- 7582950732103932491 is not a prime as it is divisible by 19 and 79
7582950732103932491= 19×73×5467159864530593 (3 prime factors)
19 is a Gaussian prime too.
But 73 = (8+3i)(8-3i) and the other one
5467159864530593 = (58321073 + 45451208 i) (58321073 - 45451208 i)

BTW There is a famous theorem that *every* prime of the form 4k+1 can be written as sum of two squares in *only* one way.
The reverse is also true - that is if a number (of the type 4k+1) can not be written as sum of two squares (or can be written in more than one way) then it is not a prime.

This for example 13 (only way is 3^2+2^2) is prime but 21 is not, neither is 65 (Because 65 = 64+1 =49+16)...
We have discussed this in brf before btw..

skumar wrote:
Enjoyed this but it is and it is not "simple arithmetic"

To be honest other than adding/subtracting/multiplying/dividing we have NOT used any other technique.
(I don't have to use "i" just the fact that 17=4^2+1^2 and 5^2 = 2^2+1 which is indeed "simple" arithmetic )

Okay..a slight change in the previous problem. Can you find a solution(s) when the body diagonal of the is 2023 and one of the face of the box (actually then they will be two faces as they come in pair is a square.
(Python or Excel could be used and it may be fun but not needed).
a^2+a^2+b^2 =2023 and a,b,c are integers.

2023^2-b^2 is even, so b has to be odd

So b ends in 1, 3, 5, 7, 9

b^2 ends in 1, 9, 5, 9, 1

2023^2-b^2 ends in 8, 0, 4, 0, 8

But 2023^2-b^2=2*a^2

So a^2 ends in 4/9, 0/5, 2/7, 0/5, 4/9

a^2 can't end in 2 or 7 for any a, so that rules out b ending in 5

b has to end in 1, 3, 7, or 9

a^2 ending in 4 implies that a ends in 2 or 8

a^2 ending in 9 implies that a ends in 3 or 7

a^2 ending in 0 implies a ending in 0

a^2 ending in 5 implies a ending in 5
----------But if a ends in 5, a^2 will end in 25, which means 2*a^2 will end in 50
----------But 2023^2 ends in 529, so if 2*a^2 ends in 50, b^2 will have to end in 79, which is not possible (b^2 will not be 8k+1 for any integer k)
----------So that rules out a ending in 5, a can only end in 2, 3, 7, 8, or 0

a ending in 3 or 7 implies that a^2 will be of the form 8k+1, so 2*a^2 will be of the form 8k+2, so 2*a^2+b^2 (with b being odd) will be of the form 8k+3, which can't be a perfect square. So a can only be even. That rules out a ending in 3 or 7, and a can only end in 2, 8, or 0.

OOPS, LOGICAL FALLACY IN RED TEXT, WILL REDO, OTHERS FEEL FREE TO CONTINUE THE REASONING OK fixed.

At that point I got stuck and tried combinations of a ending in 2, 8, or 0, and got two solutions in Excel:

a=168, b=2009

or

a=1428, b=119

Will try to develop the logic beyond the red text above.

Sudarshanji, Yes there are only *2* solutions, and two solutions given by you are the only ones - one can prove that.
This is why math is fun -- With Brhamgupta's Blessings, Next step after using 1 we use 2
As in noticing:
17=(4+√(−1)) (4−√(−1) )
17=(3+2⋅√(−2))(3−2⋅√(−2))

Rest is easy!

All primes of the form 8k+1 or 8k+3 can be written as a^2+2b^2.
7 can not be written in this form, but 17=3²+2⋅2²
So
Using Brahmgupta's formula: -- (a²+2b²)²=(a²−2b²)²+2(2ab)²

We get 17²=1²+2⋅12²
and 17⁴=287²+2⋅24²
Thus : two solutions only:
2023²=(7⋅17⋅1)²+2(7⋅17⋅12)² = 119^2+2*1428^2
and 2023²=(7⋅287)²+2(7⋅24)² = 2009^2+ 2*168^2

Is there a way to chat with chatGPT without giving your phone # (to access it) ? I'm not giving them my phone # (did not want to create a new account either but then caved in and used an existing account with Satya's company).

This is what ChatGPT says:

Yes, there are several ways to interact with ChatGPT without providing your phone number.

One way is to use the OpenAI website, where you can type in your queries and receive responses from ChatGPT in real-time.
Another way is to use a pre-built integration or API that allows you to communicate with ChatGPT programmatically without the need to provide your phone number.
There are also several third-party platforms, such as chatbot builders, that allow you to use ChatGPT as the underlying language model for a chatbot, and you can interact with the chatbot through their website or mobile app without providing your phone number.

Additionally, you can use the pre-built integrations that are available for different platforms like slack, discord, or any other communication platforms to interact with the model.

Please let me know if there is any other way you have in mind.

Edited at request of Amber G

*deleted*

Good Morning!

Amber G. wrote:This is what ChatGPT says:

Yes, there are several ways to interact with ChatGPT without providing your phone number.

One way is to use the OpenAI website, where you can type in your queries and receive responses from ChatGPT in real-time.
Another way is to use a pre-built integration or API that allows you to communicate with ChatGPT programmatically without the need to provide your phone number.
There are also several third-party platforms, such as chatbot builders, that allow you to use ChatGPT as the underlying language model for a chatbot, and you can interact with the chatbot through their website or mobile app without providing your phone number.

Additionally, you can use the pre-built integrations that are available for different platforms like slack, discord, or any other communication platforms to interact with the model.

Please let me know if there is any other way you have in mind.

Dhnayavaad. Much appreciated.