BR Maths Corner-1
Re: BR Maths Corner-1
AmberGji,
Looked up wikepedia for the problem.I am just stunned by the simple statement of the problem(though not obvious) and the techniques used.
Thanks for posting it.Its sort of tribute to the richness of patterns even in such simple recurrence relations.Being a SDRE madrassa math type,it just made me wonder about the minds that think of such problems,the civilisations that value them etc.
Looked up wikepedia for the problem.I am just stunned by the simple statement of the problem(though not obvious) and the techniques used.
Thanks for posting it.Its sort of tribute to the richness of patterns even in such simple recurrence relations.Being a SDRE madrassa math type,it just made me wonder about the minds that think of such problems,the civilisations that value them etc.
Re: BR Maths Corner-1
Re: BR Maths Corner-1
I agree.But the problem has been posed in a chankian way.matrimc wrote:AmberG ji slipped in an unsolved conjecture. That's cruel
Here is a challenge for BRFites... see who can find a starting number which has the longest (among BRFitest) chain before the sequence reaches 1
Re: BR Maths Corner-1
Sv et el - Thanks. Yes, the problem is *very* famous. Known as "3n+1 problem" or "Hailstone numbers" (because the values typically go up and down somewhat like a hailstone inside a cloud before finally falling to ground) or "Collatz Problem". As SV mentioned this shows the beauty of mathematics for young people.. (Erods is famous for making the problem popular)
One of the nicest treatment is in the book
Wonders of Numbers: Adventures in Math, Mind, and Meaning (It has a whole chapter devoted to 3n+1 problem)
We do know that for all positive numbers (up to some thing like 10^18 ) tried one eventually gets to 1!
(This kind has been basis of many other beautiful problems, some much easier to solve, over the last many decades)
Re: BR Maths Corner-1
I don't know if this indeed a "chankian way" but I knowingly put it that way because I thought it will be fun to try python (or your favorite computer language) to try to get "longest chain".. there may be some interesting pattern to discover...svenkat wrote:....
I agree.But the problem has been posed in a chankian way.Here is a challenge for BRFites... see who can find a starting number which has the longest (among BRFitest) chain before the sequence reaches 1
Put another way, can you find a chain which is longer than, say 1000 (or more).. answer to this may be hard (if one uses computer) or easy (if one uses logic)..
(If there is some interest, I may add a few more comments, and personal anecdote later. )
Also FWIW, change the problem just a little. Instead of "3n+1" substitute "3n-1".. what happens now? Answer may surprise you. (If you have not heard it before, resist wiki for a while before really trying a few examples..)
Re: BR Maths Corner-1
There are cycles, first cycle is at 5.Amber G. wrote: Also FWIW, change the problem just a little. Instead of "3n+1" substitute "3n-1".. what happens now? Answer may surprise you. (If you have not heard it before, resist wiki for a while before really trying a few examples..)
Proceeding in the same vein, what about
if (2 divides n) then n = n/2
else if (3 divides n) then n = n/3
else n = 5n + 1
Does it end in 1?
(edited incorrect test)
Re: BR Maths Corner-1
Here is a frame from one of my favorite comic strip:
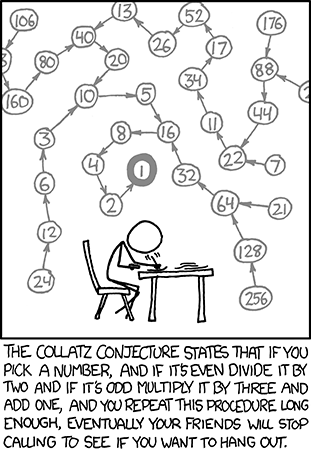

Re: BR Maths Corner-1
Obvious answer is any power of 2 which is greater than 2^1000Amber G. wrote: Put another way, can you find a chain which is longer than, say 1000 (or more).. answer to this may be hard (if one uses computer) or easy (if one uses logic)..
Re: BR Maths Corner-1
Isnt that too obvious?
Re: BR Maths Corner-1
Brilliant. Some times answers become obvious when it is pointed out.ArmenT wrote:Obvious answer is any power of 2 which is greater than 2^1000Amber G. wrote: Put another way, can you find a chain which is longer than, say 1000 (or more).. answer to this may be hard (if one uses computer) or easy (if one uses logic)..
.
Okay, now a minor modification of my original problem ..
Can you find a chain, where , say for 1000 (or more) numbers in the chain, each number is larger than the original number.
(Eg, if you take 7, you go 22,11,34,17,52,26,13,40,20,10 before you get to 5 .
Re: BR Maths Corner-1
Wild guess - 2^k - 1 for a high enough k.
Re: BR Maths Corner-1
^^ So it is still a wild guess, or has obvious logic, such as given in the case of ArmenT's example.?.
Re: BR Maths Corner-1
Still a wild guessAmber G. wrote:^^ So it is still a wild guess, or has obvious logic, such as given in the case of ArmenT's example.?.
Added later:
Outline a possible proof (not for the conjecture
To start with 2^k - 1 is odd. So we get after 2 iterations 3 * 2^(k-1) - 1 which is also odd. If the sequence of odd-even continues (this is where I am missing a step), we will get after 2i iterations 3^i* 2^(k-i) - 1 which is greater than 2^k - 1. But the conjecture is that it is going down to 1 ultimately. So at some point something happens to the odd-even sequence.
Added even later:
After 2*k steps the number becomes 3^k-1 which is even. [3^i*2^(k-i) - 1] for i < k can be shown to be odd through induction (the missing step above).
Re: BR Maths Corner-1
^^^ Yes. Once you guess 2^k-1, as you said, rest is simple.
Re: BR Maths Corner-1
Okay, here is a small problem for this month...
what is the immediate digit before and after the decimal point of (sqrt(2)+sqrt(3))^2012?
(Use calculator if you want, but it is not really needed )
)
what is the immediate digit before and after the decimal point of (sqrt(2)+sqrt(3))^2012?
(Use calculator if you want, but it is not really needed
Re: BR Maths Corner-1
matrimcji,
that was a beautiful solution.So true for K greater than or equal to 500,2^k-1 is an answer.Even your guess was a very intelligent one.
AmberGji,
this was not obvious You said you had some personal anecdote.
You said you had some personal anecdote.
that was a beautiful solution.So true for K greater than or equal to 500,2^k-1 is an answer.Even your guess was a very intelligent one.
AmberGji,
this was not obvious
Re: BR Maths Corner-1
SVenkatji, thanks
AmberG JI, I also would like to hear the anecdote.
AmberG JI, I also would like to hear the anecdote.
Re: BR Maths Corner-1
From FOM (Foundations of Mathematics) mailing list
The eminent Indologist and Sanskrit scholar Frits Staal passed away on
February 19 at his retirement home in Thailand. 'The Hindu' newspaper writes:
''Staal argued that ancient Indian grammarians, especially Panini, had
completely mastered methods of linguistic theory not discovered again until
the 1950s. The Indians had thought about it long before modern mathematical
logic was applied to linguistics by Noam Chomsky.
The early methods allowed the construction of discrete, potentially infinite
generative systems, experts maintain. The formal basis for Panini's methods
involves the use of auxiliary markers, rediscovered in the 1930s by logician
Emil Post, whose rewrite systems are currently a standard approach for
description of computer languages, experts say.
Staal wrote, 'Panini is the Indian Euclid.' The Indologist describes how
Panini had expanded the spoken Sanskrit to a formal metalanguage."
The complete piece is at
http://www.thehindu.com/news/states/ker ... 913333.ece
Among Frits' many publications, examples of possible interest to FOM readers
include 'The concept of metalanguage and its Indian background', J. Indian
Phil., 1975 3(3), pp. 315-354; and 'The Sanskrit of science,' J. Indian Phil.,
1995, 23 (1), pp. 73-127. Among his several distinguished academic positions,
Frits was a long-time faculty member of UC Berkeley's Group in Logic and the
Methodology of Science, created by Alfred Tarski.
John Kadvany
Re: BR Maths Corner-1
^^^One of the main specialty of Staal was "Śulba Sūtras" (of Vedic Sanskrit) which contained (or is source of) lot of interesting mathematical problems. Pythagorean Theorem ( wrt to the construction of sacrificial fire altars - according to Staal was mentioned) and Binomial Theorem, and Fibonacci numbers (I have some posts wrt to it's relation to sanskrit sloka metering).. had origin there. Berkeley did have/has one of good dept for such things. ..
These two references are taken from wiki:
Staal, Frits (1999), "Greek and Vedic Geometry", Journal of Indian Philosophy, 27 (1–2): 105–127,
Staal, Frits (2001), "Squares and oblongs in the Veda", Journal of Indian Philosophy,
These two references are taken from wiki:
Staal, Frits (1999), "Greek and Vedic Geometry", Journal of Indian Philosophy, 27 (1–2): 105–127,
Staal, Frits (2001), "Squares and oblongs in the Veda", Journal of Indian Philosophy,
Re: BR Maths Corner-1
Speaking of Erdos ... There was a fairly well known problem ( google for "discrepancy problem") where he offered $500 for the solution ..
One of the problem in this week's US math Olympics (for high school students) was based on that .. may post here later.
One of the problem in this week's US math Olympics (for high school students) was based on that .. may post here later.
Re: BR Maths Corner-1
AmberG,
In Bhadrachalm, Andhra Pradesh, they are performing this week, "Athirathram-2012" a Vedic ritual that late Dr. Frits Staal had helped document a few years ago. See the link in the Epics thread in GDF.
In Bhadrachalm, Andhra Pradesh, they are performing this week, "Athirathram-2012" a Vedic ritual that late Dr. Frits Staal had helped document a few years ago. See the link in the Epics thread in GDF.
Re: BR Maths Corner-1
^^^ Here is an old and famous related problem from that era. Many versions of the problem exist, so sorry if you have heard it before. You may still have fun solving it...
***
Three brothers and a bandar (monkey) had a a pile of jamuns (a kind of berry) . At night one of the brother came to the pile of jamuns while the others were asleep and, finding that there was just one more jamun than could be exactly divided by three, tossed the extra jamun to the monkey and took away one third of the remainder. Then he went back to sleep. Presently another one of them woke up and went to the pile of jamuns. He also found just one too much to be divided by three so he tossed the extra one to the monkey, took one third of the remainder, and returned to sleep. After a while the third rose, and he too gave one jamun to the monkey and took away the whole number of jamuns which represented precisely one third of the rest. Next morning the 3 brothers got up and went to the pile. Again they found just one too much, so they gave one to the monkey and divided the rest evenly. What is the least number of jamuns with which this can be done?
****
The problem is still used to introduce a very interesting concept.. curious if any one has a comment, or seen the problem before.
***
Three brothers and a bandar (monkey) had a a pile of jamuns (a kind of berry) . At night one of the brother came to the pile of jamuns while the others were asleep and, finding that there was just one more jamun than could be exactly divided by three, tossed the extra jamun to the monkey and took away one third of the remainder. Then he went back to sleep. Presently another one of them woke up and went to the pile of jamuns. He also found just one too much to be divided by three so he tossed the extra one to the monkey, took one third of the remainder, and returned to sleep. After a while the third rose, and he too gave one jamun to the monkey and took away the whole number of jamuns which represented precisely one third of the rest. Next morning the 3 brothers got up and went to the pile. Again they found just one too much, so they gave one to the monkey and divided the rest evenly. What is the least number of jamuns with which this can be done?
****
The problem is still used to introduce a very interesting concept.. curious if any one has a comment, or seen the problem before.
Re: BR Maths Corner-1
I hadn't seen the problem before, but it wasn't too hard to reverse engineer it by working backwards.
Let x = min # of jamuns that solves this problem.
In the morning, they gave one to the monkey and divided the rest into 3 equal parts. Therefore, when they woke up in the morning, they had: (x * 3 + 1) jamuns
Before this happened, the third brother gave 1 to the monkey and took his 1/3rd share. Therefore, before he did his hanky panky monkey business, there were: ( (x * 3 + 1) * 3/2 + 1) jamuns
Similarly, before second brother did his monkey business, there were ( ( (x * 3 + 1) * 3/2 + 1) * 3/2 + 1) jamuns
Similarly, before first brother did his monkey business, there were ( ( ( (x * 3 + 1) * 3/2 + 1) * 3/2 + 1) * 3/2 + 1) jamuns.
Now if we substitute x = 1 in the equation we get 18.25 jamuns were there when the night started, which isn't correct since we can't have a fraction here. Therefore our assumption that x = 1 is incorrect. So we can try x = 2 and work out what the first value should be and so on, until we get integer values at the end.
Now given that I'm a lazy chap and often flunked math in school, I figured that it would be faster for me to bang out code to work this out for me:
Running this code produces the following output:
Let x = min # of jamuns that solves this problem.
In the morning, they gave one to the monkey and divided the rest into 3 equal parts. Therefore, when they woke up in the morning, they had: (x * 3 + 1) jamuns
Before this happened, the third brother gave 1 to the monkey and took his 1/3rd share. Therefore, before he did his hanky panky monkey business, there were: ( (x * 3 + 1) * 3/2 + 1) jamuns
Similarly, before second brother did his monkey business, there were ( ( (x * 3 + 1) * 3/2 + 1) * 3/2 + 1) jamuns
Similarly, before first brother did his monkey business, there were ( ( ( (x * 3 + 1) * 3/2 + 1) * 3/2 + 1) * 3/2 + 1) jamuns.
Now if we substitute x = 1 in the equation we get 18.25 jamuns were there when the night started, which isn't correct since we can't have a fraction here. Therefore our assumption that x = 1 is incorrect. So we can try x = 2 and work out what the first value should be and so on, until we get integer values at the end.
Now given that I'm a lazy chap and often flunked math in school, I figured that it would be faster for me to bang out code to work this out for me:
Code: Select all
#!/usr/bin/env python
# Assuming that you're using python 3.xx. If you're using python 2.xx, simply remove the parens () around the
# print statement below
for x in range(1, 10):
y = ( ( ( (x * 3 + 1) * 3/2 + 1) * 3/2 + 1) * 3/2 + 1)
print(x, y)
As you can see, x = 7 gives us an integral value at the end of the calculation. Now that we know what the value of x is and the total at the beginning of the night (which is 79), we can also work the calculation forwards as stated by the original problem and verify that it is indeed correct.1 18.25
2 28.375
3 38.5
4 48.625
5 58.75
6 68.875
7 79.0
8 89.125
9 99.25
Re: BR Maths Corner-1
Was the bandar raiding the jamun cache? How come the cache was alwasy one jamun short!
ArmenT, Good use of python. My son is learning it too and says its very powerful.
ArmenT, Good use of python. My son is learning it too and says its very powerful.
Re: BR Maths Corner-1
ArmenT: Your answer 79 is correct. It is *very* easy now to get other solutions of larger numbers if one wants to.
The problem is extremely well known, except some words in it, are changed a little, (or instead of 3 brothers you have more etc) when the problem is asked now a days.
I was asked this problem from my father, long ago, when I was in elementary school and I was able to do it fairly quickly, without using pen or paper (or python for that matter). (my father was very impressed by my method) . so if one thinks in the right way it, one gets the answer in fairly obvious way, and the problem can provide some beautiful insight into math.
for that matter). (my father was very impressed by my method) . so if one thinks in the right way it, one gets the answer in fairly obvious way, and the problem can provide some beautiful insight into math.
The problem is extremely well known, except some words in it, are changed a little, (or instead of 3 brothers you have more etc) when the problem is asked now a days.
I was asked this problem from my father, long ago, when I was in elementary school and I was able to do it fairly quickly, without using pen or paper (or python
Ramanji, I translated it into bandar/monkey but word used in the original text, I believe, was 'Vanar' ( a word used for Hanuman or Sugrive ) .. but the above sentence could possibly give a nice hint to solve the problem without python..ramana wrote:Was the bandar raiding the jamun cache? How come the cache was alwasy one jamun short!
Re: BR Maths Corner-1
One can easily see that you can add 3^4 = 81 to 79 to get the next answer 160 (and 241 etc..It is *very* easy now to get other solutions of larger numbers if one wants to
Re: BR Maths Corner-1
Lest we short-shrift the usefulness of computations for Mathematics in general, here is a nice panoramic view of Experimental MathematicsArmenT wrote: Now given that I'm a lazy chap and often flunked math in school, I figured that it would be faster for me to bang out code to work this out for me:
Mathematics in the Age of the Turing Machine by Thomas Hale of Pittsburg (PDF ~ 1.5MB)
Haven't finished reading, but so far has given several examples of how visualization and number theory computer experiments helped in discovering new mathematical facts.
(added further thoughts) Previously I was not convinced that visualization is as important as it is made out to be. IMHO, there is a tremendous waste of resources (computing cycles including Supercomputer cycles at various Super-computing centers) which are expended today to make eye candy for Physical/Chemical/Biological sciences.
I hope I am wrong and this particular paper my convince me to think otherwise.
Re: BR Maths Corner-1
Another thing to note is there is a pattern that emerges as we calculate the answers for values of x. As you can see from the first few results, the difference is 10.125 for consecutive values of x and therefore it will reach a whole number every 8 terms (I didn't calculate for x = 0 in my original code, but it is easy to see that the result for that would have been 8.125). Since the eighth term in the series, (i.e. x=7) produces a whole number, so will x=15, 23, 31 .... (n*8 - 1). This pattern makes it real easy to compute subsequent values that are larger number solutionsAmber G. wrote:One can easily see that you can add 3^4 = 81 to 79 to get the next answer 160 (and 241 etc..It is *very* easy now to get other solutions of larger numbers if one wants to
Progress towards Goldbach conjecture for odd numbers
From the abstract of Tao's paper: Every odd number greater than 1 is the sum of at most five primes
Looks like computations did play an important role.Our argument relies on some previous numerical work, namely the verification of Richstein of the even Goldbach conjecture up to $4 \times 10^{14}$, and the verification of van de Lune and (independently) of Wedeniwski of the Riemann hypothesis up to height $3.29 \times 10^9$.
Re: Progress towards Goldbach conjecture for odd numbers
Once we talk about the validity (truth/falsity) of theorems we invariably enter into the domain of semantics which clearly is the umbrella under which programming languages operate. Using computations to strengthen mathematical conjectures may not be such a bad idea after all!matrimc wrote:Looks like computations did play an important role.
Re: Progress towards Goldbach conjecture for odd numbers
Kasturi garukasthuri wrote:Once we talk about the validity (truth/falsity) of theorems we invariably enter into the domain of semantics which clearly is the umbrella under which programming languages operate. Using computations to strengthen mathematical conjectures may not be such a bad idea after all!
Please take a look at the paper by Thomas Hales (I posted the link a few posts back). He almost proved Kepler's conjecture and has program to put the proof into a theorem prover (HOL Light).
Re: Progress towards Goldbach conjecture for odd numbers
^^^ Very interesting...thank you for the pointer. I am not following the advances on automated theorem provers as I used to. Btw, does anybody here know where axiomatization of physics stands now (Hilbert's sixth problem?) Has it been actively pursued?
Re: BR Maths Corner-1
Okay Just for fun -
I am going to ask a few questions about an equation which made my son, and probably many others, fascinated with math...
(Result is extremely well known and is an important result, but for some reason it is still unfamiliar to most college kids..)
What is the sum of this series?
1 + 1/4 + 1/9 + 1/16 + 1/25 + 1/36 .....
(Denominator are squares of 1,2,3,4 ....)
Some very easy, some some what easy and some not so easy .. questions:
1 - Is this series convergent ? (That is, the sum is less than some number, no matter how many terms of the series one adds)
2. - If convergent, can you prove (in easy way - say not using calculus) that sum is less than xxx ... (or if that is not true, can you show it that it is not true. ( that is, the series diverges - sum tends to infinity)
3. - If convergent what is the value..? Can you show that using some simple method?
4 - Why one connects Ramanujan's name with this series ?
5. Has any Indian Mathematician solved it? ( Who was first to solve this?)
(If you have not seen this before, try to work out before checking wiki etc..)
Comments are okay to put.. (Fairly well know problem so no need for "tiny" print)
I am going to ask a few questions about an equation which made my son, and probably many others, fascinated with math...
(Result is extremely well known and is an important result, but for some reason it is still unfamiliar to most college kids..)
What is the sum of this series?
1 + 1/4 + 1/9 + 1/16 + 1/25 + 1/36 .....
(Denominator are squares of 1,2,3,4 ....)
Some very easy, some some what easy and some not so easy .. questions:
1 - Is this series convergent ? (That is, the sum is less than some number, no matter how many terms of the series one adds)
2. - If convergent, can you prove (in easy way - say not using calculus) that sum is less than xxx ... (or if that is not true, can you show it that it is not true. ( that is, the series diverges - sum tends to infinity)
3. - If convergent what is the value..? Can you show that using some simple method?
4 - Why one connects Ramanujan's name with this series ?
5. Has any Indian Mathematician solved it? ( Who was first to solve this?)
(If you have not seen this before, try to work out before checking wiki etc..)
Comments are okay to put.. (Fairly well know problem so no need for "tiny" print)
Last edited by Amber G. on 19 May 2012 16:09, edited 1 time in total.
Re: BR Maths Corner-1
Also, recently saw a variant of the problem I posted here ... (Going back to one of the very first problem which many found fun, and had a really cool elementary solution posted later (see the early part of the thread))
<problem appears here>
<Solution is here>
In general we shown that if
S = (1/2)(3/4)(5/6) ...... ((2n-1)/2n)
Then sqrt(1/4n) =< S = sqrt(1/2n) ...
(We proved that using simple method)
Can one improve this (again with elementary methods)
sqrt(1/4n) =<S < sqrt(1/3n)
(Answer, for large n is of course approx sqrt (1 / pi * n) ) why?
<problem appears here>
<Solution is here>
In general we shown that if
S = (1/2)(3/4)(5/6) ...... ((2n-1)/2n)
Then sqrt(1/4n) =< S = sqrt(1/2n) ...
(We proved that using simple method)
Can one improve this (again with elementary methods)
sqrt(1/4n) =<S < sqrt(1/3n)
(Answer, for large n is of course approx sqrt (1 / pi * n) ) why?
Last edited by Amber G. on 19 May 2012 16:12, edited 2 times in total.
Re: BR Maths Corner-1
Okay .. There was a hint when I said the original problem had the word वानर (Vanar).. (Thanks Ramana - what else a vanar will do with a jamun cache ? !)ArmenT wrote:One can easily see that you can add 3^4 = 81 to 79 to get the next answer 160 (and 241 etc.. >>Amber G. wrote:>> It is *very* easy now to get other solutions of larger numbers if one wants to
Another thing to note is there is a pattern that emerges as we calculate the answers for values of x. As you can see from the first few results, the difference is 10.125 for consecutive values of x and therefore it will reach a whole number every 8 terms (I didn't calculate for x = 0 in my original code, but it is easy to see that the result for that would have been 8.125). Since the eighth term in the series, (i.e. x=7) produces a whole number, so will x=15, 23, 31 .... (n*8 - 1). This pattern makes it real easy to compute subsequent values that are larger number solutions. Guess that's one more instance of "computer-aided-pattern-recognition" (copyright matrimc, who first mentioned it after I detected a pattern in this post and used it to solve the problem).
A vedic vanar, actually some times, gives a jamun (instead of taking one) ..
In that case answer you will see is 2 jamuns ..
(vanar giving a jamun makes it 3, when one brothers eats 1, you are left again with 2 jamuns and the whole thing can repeate..)
So now we do not have vedic vanar. Instead we have a bandar who takes 1 jamun (instead of doing the good deed - Even the crocodiles know that bandars actually pick jamuns - remember panchatantra
But we do have vedic math ..
So answer is .. drum roll.... -2 (negative 2 jamuns)
Check it out, it works...
Ok so you live in kali yug which has no negative jamuns ..
But we know, we can always add 3^4 = 81 to any answer...
-2 + 81 = 79
Same answer given by kaliyug computers .. which are a little slower.
(This was more or less my method when I first heard the problem when I was quite young)
Hope this is fun.
BTW
ArmenTji we should all remember who invented "zero" so when you said:
[quote](I didn't calculate for x = 0 in my original code, but it is easy to see that the result for that would have been 8.125)[/quote]
If you did calculate the case for x=0, better if you have gone back one more ...even a kaliyug computer would have found the indic answer -2
Re: BR Maths Corner-1
Schoolboy cracks age-old maths problem
 .
.
AmberG ma'am: I'm still not certain about how you derived 3^4 or the -2. What's that got to do with the word "vanar" anyway? Would you please mind explaining in simple terms if it isn't too much of a bother (Sorry for any trouble caused, I'm not really all that good at math, but I like puzzles anyway -- it's kinda like scratching an itch).
Incidentally, for all the link language lawyers, this kid wrote his paper in GermanA 16-year-old schoolboy has solved a mathematical problem which has stumped mathematicians for centuries, a newspaper report said. The boy put the historical breakthrough down to “schoolboy naivety.”
Shouryya Ray, who moved to Germany from India with his family at the age of 12, has baffled scientists and mathematicians by solving two fundamental particle dynamics problems posed by Sir Isaac Newton over 350 years ago, Die Welt newspaper reported on Monday.
AmberG ma'am: I'm still not certain about how you derived 3^4 or the -2. What's that got to do with the word "vanar" anyway? Would you please mind explaining in simple terms if it isn't too much of a bother (Sorry for any trouble caused, I'm not really all that good at math, but I like puzzles anyway -- it's kinda like scratching an itch).
Re: BR Maths Corner-1
I have a question in linear algebra which I have been brain-storming for days - and I thought I will resort to help.
Suppose that we have two finite dimensional Hilbert spaces H1 and H2. I need to construct a basis B for
H = H1 direct-sum H2
such that for any two vectors D1,D2 in H1, vectors E1,E2 in H2 and representation V1 of (D1,E1) on B and representation V2 of (D2,E2) on B, if V1 and V2 are "close" then, D1 should be "close" to E1 *and* D2 should be "close" to E2.
In other words, B should "preserve" the variance in the respective spaces.
I think such problems would have been encountered in physics (QM) where one needs a frame of reference that preserves the variance (I am really vague here, sorry). So physics intuitions are highly welcome...
Also, any help in further refining the problem will be greatly appreciated...and I promise you will be a co-author on the paper if it leads to something, which I think it will {added later: as this is a good problem to solve in genomics}.
Added later:
"representation V1 of (D1,E1) on B and representation V2 of (D2,E2) on B" means "coordinates V1 of (D1,E1) on B and coordinates V2 of (D2,E2) on B"
Suppose that we have two finite dimensional Hilbert spaces H1 and H2. I need to construct a basis B for
H = H1 direct-sum H2
such that for any two vectors D1,D2 in H1, vectors E1,E2 in H2 and representation V1 of (D1,E1) on B and representation V2 of (D2,E2) on B, if V1 and V2 are "close" then, D1 should be "close" to E1 *and* D2 should be "close" to E2.
In other words, B should "preserve" the variance in the respective spaces.
I think such problems would have been encountered in physics (QM) where one needs a frame of reference that preserves the variance (I am really vague here, sorry). So physics intuitions are highly welcome...
Also, any help in further refining the problem will be greatly appreciated...and I promise you will be a co-author on the paper if it leads to something, which I think it will {added later: as this is a good problem to solve in genomics}.
Added later:
"representation V1 of (D1,E1) on B and representation V2 of (D2,E2) on B" means "coordinates V1 of (D1,E1) on B and coordinates V2 of (D2,E2) on B"
-
vina
- BRF Oldie
- Posts: 6046
- Joined: 11 May 2005 06:56
- Location: Doing Nijikaran, Udharikaran and Baazarikaran to Commies and Assorted Leftists
Re: BR Maths Corner-1
Amber G. wrote:Okay Just for fun -
I am going to ask a few questions about an equation which made my son, and probably many others, fascinated with math...
(Result is extremely well known and is an important result, but for some reason it is still unfamiliar to most college kids..)
What is the sum of this series?
1 + 1/4 + 1/9 + 1/16 + 1/25 + 1/36 .....
(Denominator are squares of 1,2,3,4 ....)
Some very easy, some some what easy and some not so easy .. questions:
Yes1 - Is this series convergent ? (That is, the sum is less than some number, no matter how many terms of the series one adds)
Yes. Less than 22. - If convergent, can you prove (in easy way - say not using calculus) that sum is less than xxx ... (or if that is not true, can you show it that it is not true. ( that is, the series diverges - sum tends to infinity)
Sorry. Could do it if I was back in the Madrassa. Addled now. But yes, piece wise integration of the RHS and summing should give you the answer.3. - If convergent what is the value..? Can you show that using some simple method?
4 - Why one connects Ramanujan's name with this series ?
Dunno
5. Has any Indian Mathematician solved it? ( Who was first to solve this?)
(If you have not seen this before, try to work out before checking wiki etc..)
Comments are okay to put.. (Fairly well know problem so no need for "tiny" print)[/quote]
Re: BR Maths Corner-1
But 2^n > n^2 for all n >vina wrote:Yes. Less than 2
Added later:
Theek hai, Vina is correct. In the first four terms, Sigma(1/2^n) is