This could go both in Physics and Math dhaga .. An exciting discovery in finding elegant proof in Math,, inspired by results from physicists. Wow!
Three physicists wanted to calculate how neutrinos change. They ended up discovering an unexpected relationship between some of the most ubiquitous objects in math. Basic Math.
See details in physics dhaga.
BR Maths Corner-1
Re: BR Maths Corner-1
xpost from physics dhaga
Re: BR Maths Corner-1
Since we were talking about Collatz Conjecture a couple of years (maybe more time has passed, I don't remember), here is some nice result by Terence Tao.
Summary of the result: Prof. Tao proves that if the starting numbers are greater than one quadrillion, 99% of those numbers become smaller than 200.
I think this approach can be used to prove probabilistic results in Number Theory.
Here is the link
https://www.quantamagazine.org/mathemat ... -20191211/
Summary of the result: Prof. Tao proves that if the starting numbers are greater than one quadrillion, 99% of those numbers become smaller than 200.
I think this approach can be used to prove probabilistic results in Number Theory.
Here is the link
https://www.quantamagazine.org/mathemat ... -20191211/
Re: BR Maths Corner-1
^^Thanks for posting, yes we have talked about this here.. (also known as 3k+1 problem).
Basically it is easy to state (and has been a basis for a few math problems)
- start with any number.
- If it is even divide by half
- If it is odd multiply be 3 and add 1
Repeat above with the new number you got.. what will happen? ( For example if you start with 7 it goes ->22 -> 11->34 ->17 ->52 ->26 -> 13 -> 40 -> 20 -> 10 -> 5 -> 16 -> 8 -> 4 -> 2 ->1 and then repeats 4,2,1 ...). Does this happen all the time?
Basically it is easy to state (and has been a basis for a few math problems)
- start with any number.
- If it is even divide by half
- If it is odd multiply be 3 and add 1
Repeat above with the new number you got.. what will happen? ( For example if you start with 7 it goes ->22 -> 11->34 ->17 ->52 ->26 -> 13 -> 40 -> 20 -> 10 -> 5 -> 16 -> 8 -> 4 -> 2 ->1 and then repeats 4,2,1 ...). Does this happen all the time?
Re: BR Maths Corner-1
Happy 2020!
Here is something some may find amazing.
By using all the integers from 1 to 9 you get a very good approximation for e which is accurate up to about 10^26 (18457734525360901453873570 ) decimal DIGITS!
The result was found by mathematician R. Sabey in 2004.
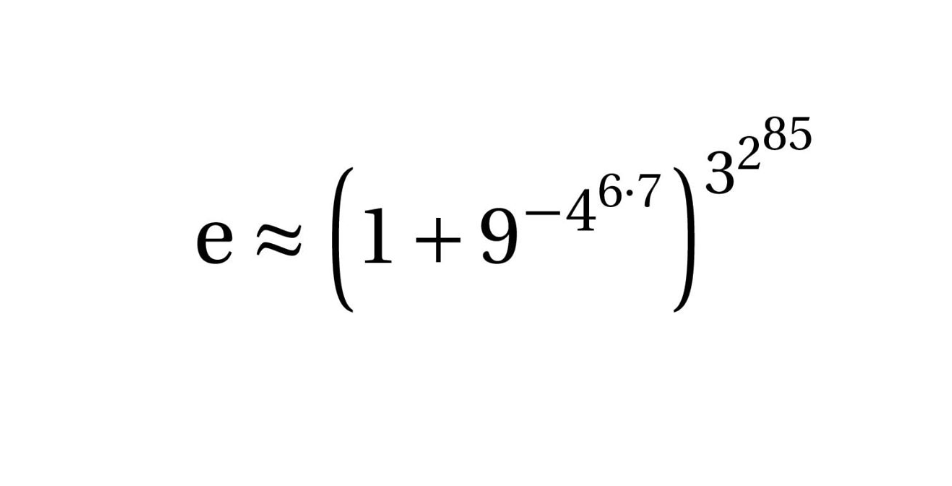 It is not too hard to verify this. Try it you will enjoy it.
It is not too hard to verify this. Try it you will enjoy it.
Note "6.7" above is 6 multiplied by 7 (or42)
Here is something some may find amazing.
By using all the integers from 1 to 9 you get a very good approximation for e which is accurate up to about 10^26 (18457734525360901453873570 ) decimal DIGITS!
The result was found by mathematician R. Sabey in 2004.
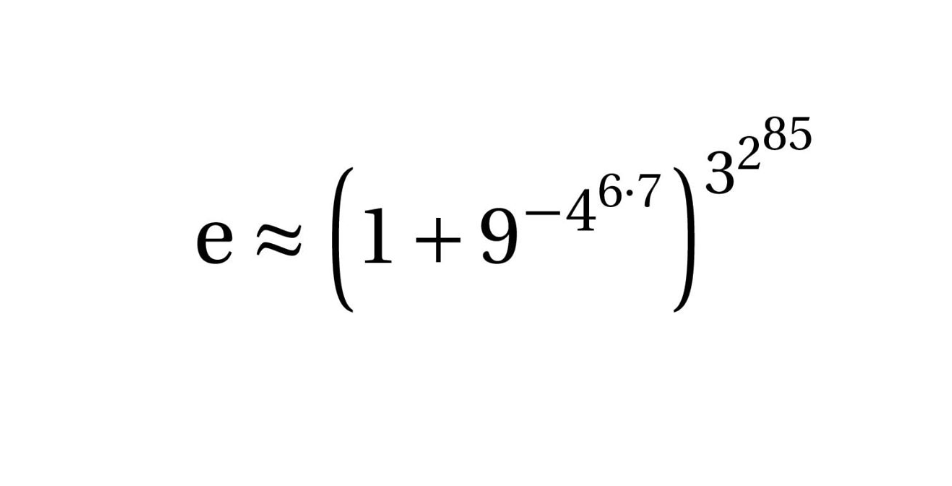 It is not too hard to verify this. Try it you will enjoy it.
It is not too hard to verify this. Try it you will enjoy it. Note "6.7" above is 6 multiplied by 7 (or42)
Re: BR Maths Corner-1
That's clever, I can see how it works (series expansion, and a creative use of the 9, 4, 6, 7, 3, 2, and 85 - that part was neat). Basically the second term within the brackets, is the inverse of the exponential term - this is the key. I can kind of verify how many digits of precision it would give you - if I went with logarithms, I can figure out what the error would add up to - 3^(2^85) ~= 3^(10^28) ~= 10^(5*10^27) - so I guess we kind of get the 10^26 decimal places of precision right there.Amber G. wrote:Happy 2020!
Here is something some may find amazing.
By using all the integers from 1 to 9 you get a very good approximation for e which is accurate up to about 10^26 (18457734525360901453873570 ) decimal DIGITS!
The result was found by mathematician R. Sabey in 2004.
It is not too hard to verify this. Try it you will enjoy it.
Note "6.7" above is 6 multiplied by 7 (or42)
If we designate 3^(2^85) as X, then it's the error between (X-1)/((2!)*X), versus 1/(2!), basically - the remaining terms in the Taylor series should rapidly decline in terms of contribution to the error.
More like creative use of the digits, than a true discovery. I'm impressed at the art behind it.
But you know what, I just figured out that one can do this with all ten digits (0 to 9) by adding a 0 at any of several places in the above equation
Re: BR Maths Corner-1
"Adding 0" is nice..sudarshan wrote:That's clever, I can see how it works (series expansion, and a creative use of the 9, 4, 6, 7, 3, 2, and 85 - that part was neat). Basically the second term within the brackets, is the inverse of the exponential term - this is the key. I can kind of verify how many digits of precision it would give you - if I went with logarithms, I can figure out what the error would add up to - 3^(2^85) ~= 3^(10^28) ~= 10^(5*10^27) - so I guess we kind of get the 10^26 decimal places of precision right there.Amber G. wrote:Happy 2020!
Here is something some may find amazing.
By using all the integers from 1 to 9 you get a very good approximation for e which is accurate up to about 10^26 (18457734525360901453873570 ) decimal DIGITS!
The result was found by mathematician R. Sabey in 2004.
<equation e ≈ (1+9^4^(7*6))^3^2^85)>It is not too hard to verify this. Try it you will enjoy it.
Note "6.7" above is 6 multiplied by 7 (or42)
If we designate 3^(2^85) as X, then it's the error between (X-1)/((2!)*X), versus 1/(2!), basically - the remaining terms in the Taylor series should rapidly decline in terms of contribution to the error.
More like creative use of the digits, than a true discovery. I'm impressed at the art behind it.
But you know what, I just figured out that one can do this with all ten digits (0 to 9) by adding a 0 at any of several places in the above equation. This is my big discovery, right now (2020).
---
To me, the very definition of e (base of natural logarithm) is that it is a limiting value of (1+1/x)^x when x is very large. This is intuitive and this is how I was introduced to e and this is how I introduce e for the first time to elementary students. (compound interest problem when interest is calculated "continuously"). As you pointed out, x = 9^(4^42) = 9^(2^84) = 3^(2^85) is a VERY large number so by very definition, the whole expression is very close to e.
Re: BR Maths Corner-1
That "compound interest calculated continuously" seems like a very intuitive definition for e. Of course, the interest rate would have to be just right (as in - 1/N for a period of N years/ days/ seconds/ whatever - of course, with N being a very long interval - tending to infinity).
Re: BR Maths Corner-1
OK, so to define e for a lay person (just solidifying my own understanding of the concept):
(Pi is easy, ratio of circumference of a circle to its diameter, pretty intuitive)
e~=2.718282
So you go to a bank, and deposit Re. 1. They give you 100% interest per annum, for a year.
If this is simple interest, at the end of 1 year, you get Rs. 2. If this is compound interest, even then you get Rs. 2 after a year.
Now the bank changes its policy, they will give you 50% interest, every six months, for the duration of a year.
If this is simple interest, at the end of 1 year, you still get Rs. 2. If this is compound interest, however, you will get Rs. 2.25. So compound interest over simple, will yield you an additional 25 paise.
The bank now changes its policy to - 33.33% interest (100%/3), every four months, for the duration of a year.
Simple interest - still Rs. 2 after a year. Compound interest - roughly Rs. 2.37.
25% interest every 3 months for a year? Rs. 2, vs. Rs. 2.44 (roughly).
10% interest, 10 times a year, for a year? Rs. 2, vs. Rs. 2.59 (roughly).
1% interest, 100 times a year, for a year? Rs. 2, vs. Rs. 2.70 (roughly).
If they split up and paid the interest every second, for a year? Rs. 2, vs. Rs. 2.718282... (very close to e).
So as the interest is split and compounded over more and more intervals within the year (i.e., as the calculation becomes more and more continuous), we approach e (2.718282...).
So the "compound interest advantage over simple" is Rs. 0.718282..., or e-2.
Never thought of it that way before, but it is a great way to explain e to a lay person. Thanks for that pointer.
(Pi is easy, ratio of circumference of a circle to its diameter, pretty intuitive)
e~=2.718282
So you go to a bank, and deposit Re. 1. They give you 100% interest per annum, for a year.
If this is simple interest, at the end of 1 year, you get Rs. 2. If this is compound interest, even then you get Rs. 2 after a year.
Now the bank changes its policy, they will give you 50% interest, every six months, for the duration of a year.
If this is simple interest, at the end of 1 year, you still get Rs. 2. If this is compound interest, however, you will get Rs. 2.25. So compound interest over simple, will yield you an additional 25 paise.
The bank now changes its policy to - 33.33% interest (100%/3), every four months, for the duration of a year.
Simple interest - still Rs. 2 after a year. Compound interest - roughly Rs. 2.37.
25% interest every 3 months for a year? Rs. 2, vs. Rs. 2.44 (roughly).
10% interest, 10 times a year, for a year? Rs. 2, vs. Rs. 2.59 (roughly).
1% interest, 100 times a year, for a year? Rs. 2, vs. Rs. 2.70 (roughly).
If they split up and paid the interest every second, for a year? Rs. 2, vs. Rs. 2.718282... (very close to e).
So as the interest is split and compounded over more and more intervals within the year (i.e., as the calculation becomes more and more continuous), we approach e (2.718282...).
So the "compound interest advantage over simple" is Rs. 0.718282..., or e-2.
Never thought of it that way before, but it is a great way to explain e to a lay person. Thanks for that pointer.
Re: BR Maths Corner-1
^ Actually, it seems "e" was obtained in exactly the above way in 1683 by Bernoulli. Some websites even have the exact example I wrote above, just with "$" instead of "Rs." I had no clue all these days.
Re: BR Maths Corner-1
^^^ Very nicely explained. Thanks.
As I said, this is how I, always, introduce e to young people (who never heard of it before) and this is how I learned about it (fairly young age). It is quite intuitive. Of course it does not have to be compound interest.. anything growing exponentially (like population, germs, or lotus flowers in a lake - example I fondly remember my father giving it to me) will do. Similarly anything decaying (like radioactive decay).. here one gets (1/e).
Recently I asked my granddaughter (not going to school yet) who was asking "Alexa" to "Increase the volume by 100%" for her favorite song -- How about if you asked it "Increase the volume by 50% twice" .. or "Increase the volume by 10% 10 times" ..(or "1% hundred times ..or even 1 zillionth of a percent 100 zillion times).... Yes eventually the volume would be 271.28...% .
.
Another use of this method, young people get the understanding of concepts like convergent series and limiting value without doing any higher math. For example one can intuitively see that e is > 2 (or even 2.5 etc.. by taking sufficient smaller periods). But one can also see that e will always be less than 3. . Generally one sees this in ordinary math books by showing the series e=1+1+ 1/2+1/6+1/24+ 1/5! ... is less than 3.
(One normally does by comparing with geometric series of similar way)
However, thinking of "decay" and having starting with 1/e = 1 -1+ 1/2 - 1/6 + (small) - (smaller) + (even smaller)..
One can see that 1/e is between 1/2 and (1/2-1/6= 1/3).. IOW e is between 2 and 3 !!
****
As I said, this is how I, always, introduce e to young people (who never heard of it before) and this is how I learned about it (fairly young age). It is quite intuitive. Of course it does not have to be compound interest.. anything growing exponentially (like population, germs, or lotus flowers in a lake - example I fondly remember my father giving it to me) will do. Similarly anything decaying (like radioactive decay).. here one gets (1/e).
Recently I asked my granddaughter (not going to school yet) who was asking "Alexa" to "Increase the volume by 100%" for her favorite song -- How about if you asked it "Increase the volume by 50% twice" .. or "Increase the volume by 10% 10 times" ..(or "1% hundred times ..or even 1 zillionth of a percent 100 zillion times).... Yes eventually the volume would be 271.28...%
Another use of this method, young people get the understanding of concepts like convergent series and limiting value without doing any higher math. For example one can intuitively see that e is > 2 (or even 2.5 etc.. by taking sufficient smaller periods). But one can also see that e will always be less than 3. . Generally one sees this in ordinary math books by showing the series e=1+1+ 1/2+1/6+1/24+ 1/5! ... is less than 3.
(One normally does by comparing with geometric series of similar way)
However, thinking of "decay" and having starting with 1/e = 1 -1+ 1/2 - 1/6 + (small) - (smaller) + (even smaller)..
One can see that 1/e is between 1/2 and (1/2-1/6= 1/3).. IOW e is between 2 and 3 !!
****
Re: BR Maths Corner-1
^^^ To establish the value of e with accuracy .. (both upper and lower bound) .. one can take Sudarshanji's example above.
If we use "negative 10% interest" (loose money - like some of my investments).. 10 times a year.. and start with Rs 1.. I will have (.9)^10 about 0.349 (=1/2.87)..
So for "continuous interest".. e is strictly between 2.59 and 2.87 !!
(And this is all without using any higher math other than use of a calculator or multiplying 1.1 (or .9) 10 times)
10% interest, 10 times a year, for a year? [Rs 1 will become] Rs. 2.593 (roughly).
If we use "negative 10% interest" (loose money - like some of my investments).. 10 times a year.. and start with Rs 1.. I will have (.9)^10 about 0.349 (=1/2.87)..
So for "continuous interest".. e is strictly between 2.59 and 2.87 !!
(And this is all without using any higher math other than use of a calculator or multiplying 1.1 (or .9) 10 times)
Re: BR Maths Corner-1
106 years ago, on this date (Jan 16, 1913) Srinivas Ramanujan wrote his famous letter...

Attached with the letter were some of his results..Hope people enjoy solving them..


Attached with the letter were some of his results..Hope people enjoy solving them..

Re: BR Maths Corner-1
Featuring Jayadev Athreya on a new discovery about platonic solids, in particular dodecahedra.
Re: BR Maths Corner-1
Nice.sudarshan wrote:... If we designate 3^(2^85) as X, then it's the error between (X-1)/((2!)*X), versus 1/(2!), basically - the remaining terms in the Taylor series should rapidly decline in terms of contribution to the error.
Re: BR Maths Corner-1
^^^ A few comments..(FWIW)
In most books, e is generally *defined* as lim x->infinity (1+1/x)^x which if expanded using binomial theorem :
1 + 1 + (1/2!) (x(x-1)/x^2) + (1/3!) x(x-1)(x-2)/x^3 +...
when x tends to infinity this gives the familiar series ,,, e=1+1+1/2+1/3!+...
Also (1-1/x)^x is 1/e.
In most books, e is generally *defined* as lim x->infinity (1+1/x)^x which if expanded using binomial theorem :
1 + 1 + (1/2!) (x(x-1)/x^2) + (1/3!) x(x-1)(x-2)/x^3 +...
when x tends to infinity this gives the familiar series ,,, e=1+1+1/2+1/3!+...
Also (1-1/x)^x is 1/e.
Re: BR Maths Corner-1
On this day in 1905 Indian Mathematician Dattatreya Ramachandra Kaprekar was born. He liked numbers, and was known as “Ganitanand”. And he had lot of "fun" problems ( recreational mathematician) He is known for describing several classes of natural numbers which included Kaprekar, Harshad and Self numbers. ..
Here is sample of "Kaprekar" number (or series)..
Start with any 4 digit number (except all the digits are same)
write all digits in ascending order and subtract from this a number written in descending order..
Repeat this process...
You will reach "Kaprekar" constant of order 4 which is
For example you start with numbers say 3,3,4,7 Now do this
7433–3347 = 4086
8640–0468 = 8172
8721–1278 = 7443
7443–3447 = 3996
9963–3699 = 6264
6642–2466 = 4176
7641–1467 = 6174
No matter where you start, you will reach 6174 (unless you start with 1111 (or 2222 etc) then you will get 0)
***
(Interestingly 6174 is also a "harshad" number because it is divisible by sum of it's digits.
Here is sample of "Kaprekar" number (or series)..
Start with any 4 digit number (except all the digits are same)
write all digits in ascending order and subtract from this a number written in descending order..
Repeat this process...
You will reach "Kaprekar" constant of order 4 which is
For example you start with numbers say 3,3,4,7 Now do this
7433–3347 = 4086
8640–0468 = 8172
8721–1278 = 7443
7443–3447 = 3996
9963–3699 = 6264
6642–2466 = 4176
7641–1467 = 6174
No matter where you start, you will reach 6174 (unless you start with 1111 (or 2222 etc) then you will get 0)
***
(Interestingly 6174 is also a "harshad" number because it is divisible by sum of it's digits.
Re: BR Maths Corner-1
dup-- deleted.
Last edited by Amber G. on 18 Jan 2020 08:22, edited 1 time in total.
Re: BR Maths Corner-1
Thanks for posting it. I enjoyed playing with these regular polyhedrons..Shwetank wrote:[>>> Youtube>>> G9_l8QASobI[/youtube]
Featuring Jayadev Athreya on a new discovery about platonic solids, in particular dodecahedra.
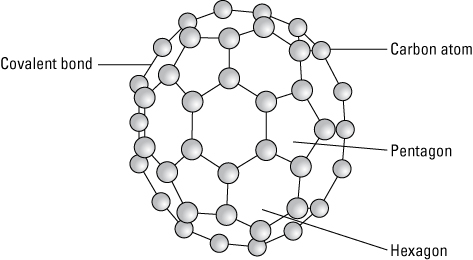
Here is an interesting fact I recently noticed (rediscovered).. (Not too hard to prove - will not put the solution here.. go ahead and put it if you find a good explanation)
In any convex solid which is made out of hexagons and pentagons only (say a soccer ball or "bucky ball type molecule) or any other shape... number of pentagons will always be 12...
For example here:
Re: BR Maths Corner-1
Have not visited BRF for a long time - have been busy with other things .. (lot of scientist are busy with this Covid thing  ))
))
OTD Ramnujan died 100 years ago. Here is a nice documentary some may enjoy.
OTD Ramnujan died 100 years ago. Here is a nice documentary some may enjoy.
Re: BR Maths Corner-1
^^^ In honor of Ramanujan, here is one less known but easy to remember fraction for pi, given by him:
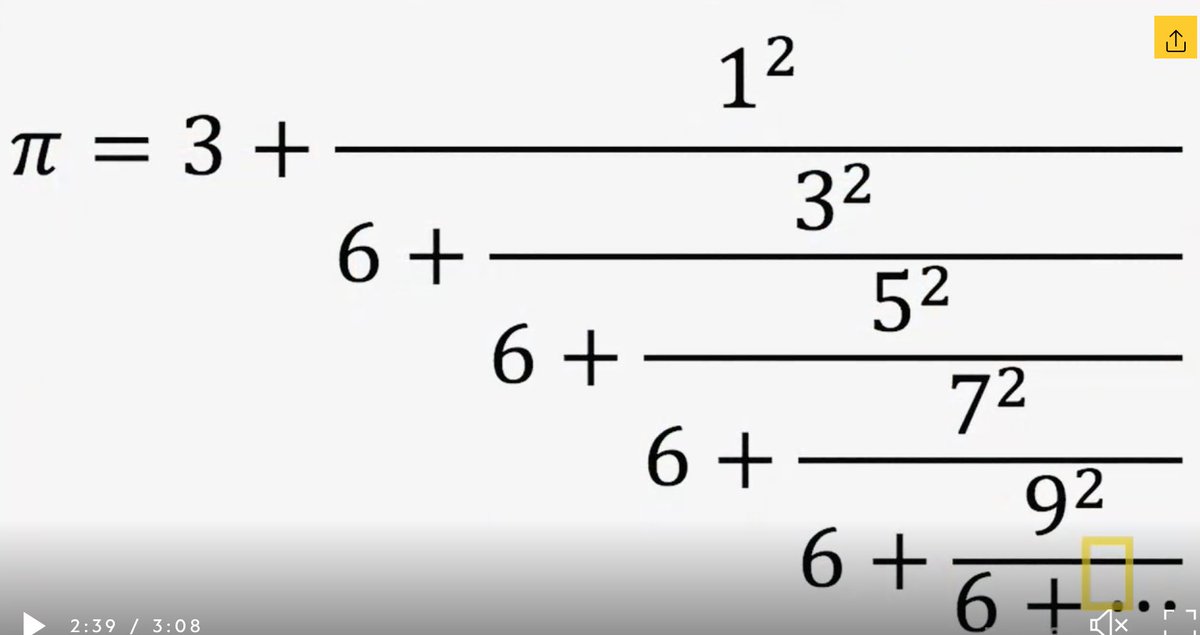
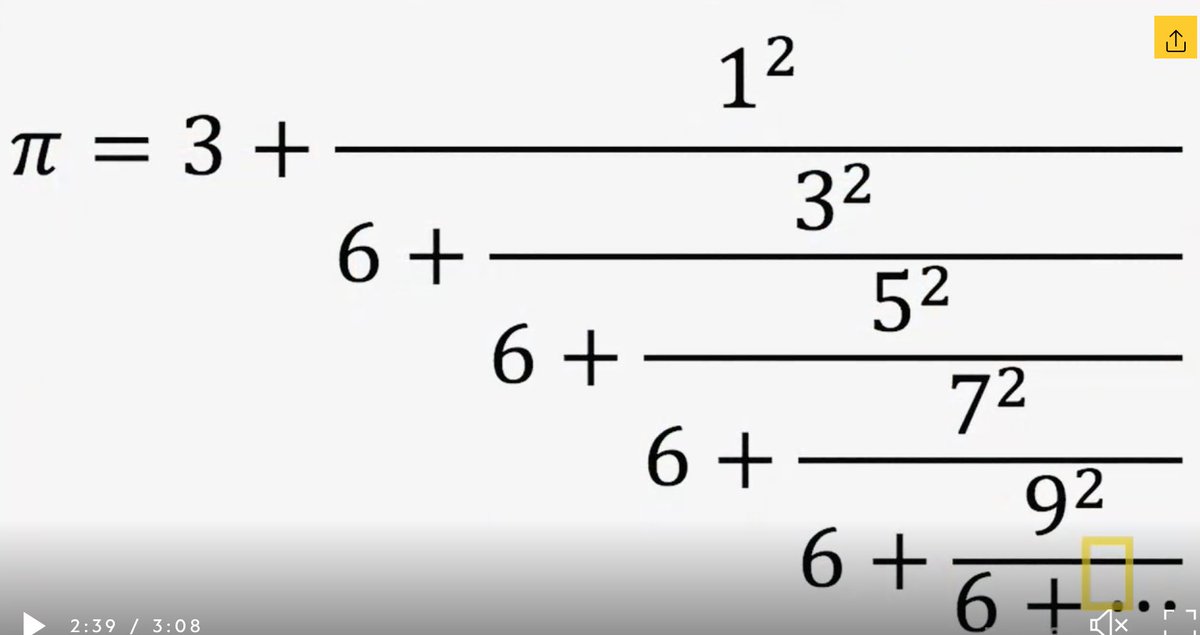
Re: BR Maths Corner-1
This enforced social distancing has given me a chance to write a lot of notes that almost form a book. The notes deal with specialized problems. More suitable for general audiences are the shorter notes which give some background to specific problems that are of very great current interest. This particular short note is an example. I have not added any references and possibly should for further reading. It deals with the Class Number Problem in Number theory initiated by Gauss and still unsolved till today. I used an approach stripping it of any background in Algebraic Number Theory and stating questions (open problems) and results using simple language that is accessible to an audience with a little Linear Algebra background of 2X2 matrices. I have put some scanty biographical and historical notes too. Some of the results quoted have passed into the public domain, since the journals in question have allowed public access to papers published in the early 1970s like H. M. Stark's 1967 paper.
https://sites.math.rutgers.edu/~chanill ... number.pdf
There may be a few small typos as I did not proof read.
https://sites.math.rutgers.edu/~chanill ... number.pdf
There may be a few small typos as I did not proof read.
Re: BR Maths Corner-1
@vsunder ji, thanks. That is great.
Re: BR Maths Corner-1
^^ Thanks
Here is the photograph of Hardy leading his team: Hardy's Mathematicals out to field against Rest of the World in 1929 at a British Science Association meeting at Oxford. Young Edward Linfoot whose theorem with Heilbronn figures in my note can be seen as part of the team. So can a young Edward Titchmarsh be seen in the photo.
https://www.theguardian.com/higher-educ ... ures#img-2
Heilbronn had escaped from Nazi Germany and was at the Univ. of Bristol where he was joined by Linfoot and that paper was written in Bristol. Hardy was about 52 when this photo was taken.
Here is the photograph of Hardy leading his team: Hardy's Mathematicals out to field against Rest of the World in 1929 at a British Science Association meeting at Oxford. Young Edward Linfoot whose theorem with Heilbronn figures in my note can be seen as part of the team. So can a young Edward Titchmarsh be seen in the photo.
https://www.theguardian.com/higher-educ ... ures#img-2
Heilbronn had escaped from Nazi Germany and was at the Univ. of Bristol where he was joined by Linfoot and that paper was written in Bristol. Hardy was about 52 when this photo was taken.
Re: BR Maths Corner-1
Here are three sets of notes written a while ago to amuse some sophomores and juniors. The first note has 3 proofs of the fact that there are infinitely many prime numbers and is to highlight Euler's proof which is the start of Analytic Number Theory as a subject in Mathematics.
The second note is to highlight the pigeonhole principle that is deceptively simple but used by Dirichlet with such power. I show one of the uses made by Dirichlet. I end with Liouville's construction of a transcendental number. To those of you who have never heard of the pigeonhole principle. Here it is. Suppose you have 7 letters in your hand and you want to distribute it to 5 mailboxes or pigeonholes or bins or dabbas or whatever you call it, then one of the bins will contain at least two letters if not more. In general if you have n letters and m bins and n>m then distributing the n letters one will find at least one bin with more than two letters. Thats it. You can prove it by induction or take it as truth. Deceptively simple but a very potent tool.
The third short note is from a long time ago on Shock waves. You know all the things they talk about in the Military forum Kaveri engine, LCA MKIA and vortex and shocks and this and that, it breaks it up into PDE and shows what is the issue for conservation systems and so on. In the Mil forum they talk about shocks causing engine flame out and this and that etc. In these notes one sees how compression and rarefaction waves are formed etc and there are pictures. The situation is very, very complicated for shocks in 3D, so it is amazing to me how cavalier people are in the Mil forum talking about these things. In my notes I just look at shocks in 1-dimension. Think of shock waves along a tube. It could be generated by an explosion or combustion etc. Riemann yes the famous Number theorist, made profound contributions to Shocks and found the Riemann invariants. No such invariants have been found for 3D shock propagation to this day, no matter what they say in the Mil forum, getting a handle on shocks in 3D is a major accomplishment. I do not talk about Riemann invariants etc, in my notes, you can find them say in Smoller's book or the book by Dafermos. The situation of Relativistic shocks is even harder and extremely difficult. Let us not worry about that, better to understand simple, model cases. These notes were all written aeons ago and are not products from the lockdown.
I am thinking of writing a set of notes on the Famous conjectures of Ramanujan, let us see if I am in the mood. I want to point out open questions also.
1. https://sites.math.rutgers.edu/~chanill ... umbers.pdf
2. https://sites.math.rutgers.edu/~chanillo/liouville.pdf
3. https://sites.math.rutgers.edu/~chanillo/shocks.pdf
The second note is to highlight the pigeonhole principle that is deceptively simple but used by Dirichlet with such power. I show one of the uses made by Dirichlet. I end with Liouville's construction of a transcendental number. To those of you who have never heard of the pigeonhole principle. Here it is. Suppose you have 7 letters in your hand and you want to distribute it to 5 mailboxes or pigeonholes or bins or dabbas or whatever you call it, then one of the bins will contain at least two letters if not more. In general if you have n letters and m bins and n>m then distributing the n letters one will find at least one bin with more than two letters. Thats it. You can prove it by induction or take it as truth. Deceptively simple but a very potent tool.
The third short note is from a long time ago on Shock waves. You know all the things they talk about in the Military forum Kaveri engine, LCA MKIA and vortex and shocks and this and that, it breaks it up into PDE and shows what is the issue for conservation systems and so on. In the Mil forum they talk about shocks causing engine flame out and this and that etc. In these notes one sees how compression and rarefaction waves are formed etc and there are pictures. The situation is very, very complicated for shocks in 3D, so it is amazing to me how cavalier people are in the Mil forum talking about these things. In my notes I just look at shocks in 1-dimension. Think of shock waves along a tube. It could be generated by an explosion or combustion etc. Riemann yes the famous Number theorist, made profound contributions to Shocks and found the Riemann invariants. No such invariants have been found for 3D shock propagation to this day, no matter what they say in the Mil forum, getting a handle on shocks in 3D is a major accomplishment. I do not talk about Riemann invariants etc, in my notes, you can find them say in Smoller's book or the book by Dafermos. The situation of Relativistic shocks is even harder and extremely difficult. Let us not worry about that, better to understand simple, model cases. These notes were all written aeons ago and are not products from the lockdown.
I am thinking of writing a set of notes on the Famous conjectures of Ramanujan, let us see if I am in the mood. I want to point out open questions also.
1. https://sites.math.rutgers.edu/~chanill ... umbers.pdf
2. https://sites.math.rutgers.edu/~chanillo/liouville.pdf
3. https://sites.math.rutgers.edu/~chanillo/shocks.pdf
Re: BR Maths Corner-1
@vsunder ji,
I quickly went through the first set. Nice stuff on Fermat's numbers. IIRC, a couple of proofs appear in the book called "Proofs From the Book". I am sure you know the history of why that title.
Paul Erdos was asked whether God knew elegant proofs for all the theorems. His answer was "I don't know whether God exists or not, but I do believe that there does exist such a book" (paraphrasing).
I quickly went through the first set. Nice stuff on Fermat's numbers. IIRC, a couple of proofs appear in the book called "Proofs From the Book". I am sure you know the history of why that title.
Paul Erdos was asked whether God knew elegant proofs for all the theorems. His answer was "I don't know whether God exists or not, but I do believe that there does exist such a book" (paraphrasing).
Re: BR Maths Corner-1
^^^^ Vayutuvan: I have updated my note on classnumber and used the simple ideas already established in the notes to prove a famous theorem of Fermat. Any prime p of the form 4k+1 or 2 can be written as a sum of two squares
p=A^2+B^2
17=4^1+1^2, 29=5^2+2^2 etc.
It can be coupled with an identity of Brahmagupta and yields a special case of Lagrange's four square theorem. Lagrange's theorem states any number n can be written as the sum of 4 squares
n=A^2+B^2+C^2+D^2
See my notes. All these results are part of the general Waring problem. Fermat's theorem and (Lagrange's theorem) have several proofs besides the elementary one in my notes for Fermat's theorem
https://sites.math.rutgers.edu/~chanill ... number.pdf
The proof I really like is actually Geometric and due to Minkowski. But the one presented in my notes is accessible to a competent High school student.
p=A^2+B^2
17=4^1+1^2, 29=5^2+2^2 etc.
It can be coupled with an identity of Brahmagupta and yields a special case of Lagrange's four square theorem. Lagrange's theorem states any number n can be written as the sum of 4 squares
n=A^2+B^2+C^2+D^2
See my notes. All these results are part of the general Waring problem. Fermat's theorem and (Lagrange's theorem) have several proofs besides the elementary one in my notes for Fermat's theorem
https://sites.math.rutgers.edu/~chanill ... number.pdf
The proof I really like is actually Geometric and due to Minkowski. But the one presented in my notes is accessible to a competent High school student.
Re: BR Maths Corner-1
Attn: For Really bright High school math students in US and India ( and their interested parents) who are looking for a summer math program:
Check out the new (online) Harvard program. Applications are due shortly. (Due date May 15)
The program, is open to *all* students (including non-us students). It is free of charge so financially it will be affordable to people in India too - though one would need some money to buy text book, and have good internet access and computer etc. (If person is selected - some financial help could be given by some well wishers for textbooks etc... )
)
I don't know how selective the program is, as it is being run for the first time but they have a finite number of mentors so APPLY EARLY as they do want to keep a low student/mentor ratio. It is different than RSI where one has to be very good to be admitted,
as they do want to keep a low student/mentor ratio. It is different than RSI where one has to be very good to be admitted,
As said the program is free of charge but the participants must have good internet access and commitment of at least 10 hours of work per week during 6 weeks session. Details are here:
https://sites.google.com/college.harvard.edu/morph/home
Check out the new (online) Harvard program. Applications are due shortly. (Due date May 15)
The program, is open to *all* students (including non-us students). It is free of charge so financially it will be affordable to people in India too - though one would need some money to buy text book, and have good internet access and computer etc. (If person is selected - some financial help could be given by some well wishers for textbooks etc...
I don't know how selective the program is, as it is being run for the first time but they have a finite number of mentors so APPLY EARLY
As said the program is free of charge but the participants must have good internet access and commitment of at least 10 hours of work per week during 6 weeks session. Details are here:
https://sites.google.com/college.harvard.edu/morph/home
Re: BR Maths Corner-1
^^^ For those who may be thinking of applying for above, here is a way to decide if this program is for you. Below is a problem. If this problem interests you and you can solve it within a short time (say 10-15 minutes) you will like the program. The problem, set for high-school level, does *not* need a calculator / computer / internet .. just pen and paper. (And though a little different from typical problem is not too difficult, if you hit the right idea(s)).
Problem:
(Example, 6*53 = 318 is not equal to 461 so 461 is not an ekadashi number)
Problem:
Definitions: Vargyog of a number is defined as, sum of square of all it's digits (written in decimal base).
For exampe Vargyog of 461 =4^2+6^2+1^2 = 16+36+1 = 53.
Ekadashi Number: is a number which is exactly 11 times it's vargyog.
Problem: Find all 3 digits Ekadashi numbers. ( with justification).
(Example, 6*53 = 318 is not equal to 461 so 461 is not an ekadashi number)
Re: BR Maths Corner-1
So now I come full circle. I finally managed to link the notes on Class number to real engineering problems of heat flow and Mechanical vibration of plates(what frequencies/eigenvalues can be allowed in a vibrating plate and what can NEVER be allowed) and even Quantum Mechanics and to even questions that appear in some branches of Computer Science. All starting from questions on quadratic forms with apparently no "relevance" to many things. In the second installment above we saw how Quadratic forms gave a simple proof of Fermat's theorem and now I show how Fermat's theorem is linked to Engineering questions on eigenmodes of vibrating plates that are clamped along the edges, heat flow, blah, blah, blah Mil forum etc etc. . The Lattice point counting problem that gets solved so easily now appears in Computer Science a lot. OK that is all I have to say now. Here is the final file.
https://sites.math.rutgers.edu/~chanill ... number.pdf
I wish books do point out such links but no book does.
https://sites.math.rutgers.edu/~chanill ... number.pdf
I wish books do point out such links but no book does.
Re: BR Maths Corner-1
Prof. Importance of quadratic forms is well known to researchers working in Numerical Optimization. While there is no book per se, at least two books come to my mind which do discuss about quadratic forms.vsunder wrote:All starting from questions on quadratic forms with apparently no "relevance" to many things.
...
I wish books do point out such links but no book does.
1. Introduction to Applied Mathematics
by Gilbert Strang | Jan 1, 1986
I think it is out of print. While it gives a broad overview of many topics, it has a somewhat chatty style as does his more famous book on Linear Algebra. I particularly did not care much for his Linear Algebra book. This one is sort of OK.
2. Combinatorial Optimization by Papadimitrou and Stiglitz also has some reference to Quadratic forms as it is an essential element to understand Interior Point Algorithms as well as whether an optimization problem is a convex optimization problem or not.
Only when the Hessian has all positive real eigenvalues, one ends up having a convex optimization problem.
Thanks for the notes though. It would be nice to have all this spelt out in a few pages rather than go through these books and/or papers
Re: BR Maths Corner-1
Okay, here is a nice problem I saw, requires just a little number theory - Based on 15th century Indian Mathematicians work..
Simplify:
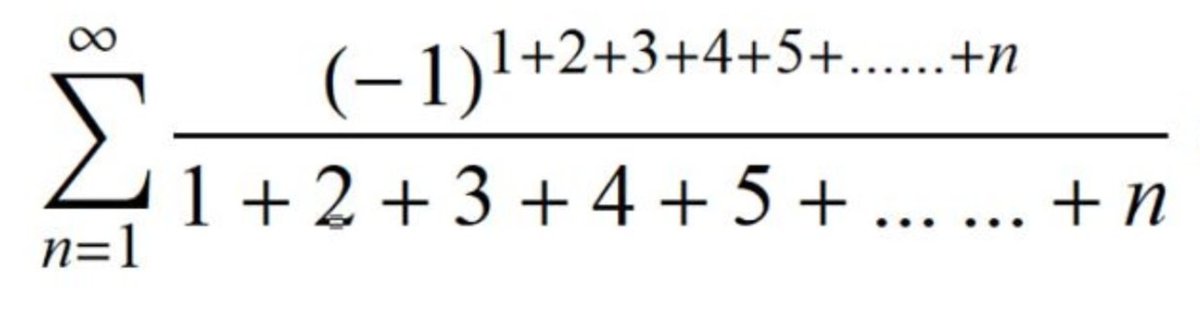
(Computer scientists can add first few hundred/thousands terms to see if they can guess the answer - actual answer is not too hard..)
Simplify:
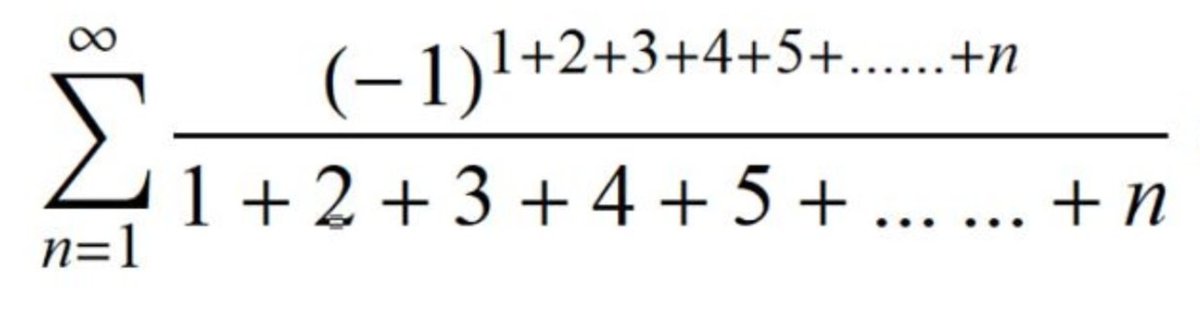
(Computer scientists can add first few hundred/thousands terms to see if they can guess the answer - actual answer is not too hard..)
Re: BR Maths Corner-1
Not sure about using number theory. But looking the terms in the series and setting off the positives from the larger negative terms led me to 3 significant terms -1 -2/15 -2/315 -.... giving me something roughly -1.14. Using the computer gave me more like -1.141 etc which looks like -pi +2.Amber G. wrote:Okay, here is a nice problem I saw, requires just a little number theory - Based on 15th century Indian Mathematicians work..
Simplify:
(Computer scientists can add first few hundred/thousands terms to see if they can guess the answer - actual answer is not too hard..)
Looking at the expression as 2*i^(n*(n-1))/(n*(n-1)) seemed promising but couldn't take it further.
Re: BR Maths Corner-1
Very Nice! Yes the answer is = -π+2Dumal wrote:Not sure about using number theory. But looking the terms in the series and setting off the positives from the larger negative terms led me to 3 significant terms -1 -2/15 -2/315 -.... giving me something roughly -1.14. Using the computer gave me more like -1.141 etc which looks like -pi +2.Amber G. wrote:Okay, here is a nice problem I saw, requires just a little number theory - Based on 15th century Indian Mathematicians work..
Simplify:
(Computer scientists can add first few hundred/thousands terms to see if they can guess the answer - actual answer is not too hard..)
Looking at the expression as 2*i^(n*(n-1))/(n*(n-1)) seemed promising but couldn't take it further.
Interestingly this problem comes from/based on Jyeṣṭhadeva's Yuktibhāṣā ( written in Malayalam almost 400 years ago around in 1530).. The answer (along with many similar serieses) is derived with the proof! - It is based on work of other Kerala mathematicians who did their work in 1400, or even 1300. (Tidbit - I saw this problem from an Indian Math prof, whose first name happens to be Srinivas (same first name as Ramanujan)...
Re: BR Maths Corner-1
Amber G. wrote:
Yes the answer is = -π+2
Interestingly this problem comes from/based on Jyeṣṭhadeva's Yuktibhāṣā ( written in Malayalam almost 400 years ago around in 1530).. The answer (along with many similar serieses) is derived with the proof! - It is based on work of other Kerala mathematicians who did their work in 1400, or even 1300. (Tidbit - I saw this problem from an Indian Math prof, whose first name happens to be Srinivas (same first name as Ramanujan)...
Will look forward to any formal solution you may be posting and especially how π comes into play. Thanks Amber-ji!
Re: BR Maths Corner-1
Thanks. Nice to see interest in Math here..Dumal wrote:
That's the first time I have ever got this far with the problems posted here all this time!

Will look forward to any formal solution you may be posting and especially how π comes into play. Thanks Amber-ji!
Yes, to me, " π comes into play" in plain looking series is still a joy. As you will see below, math part is not hard, just fun.
(Dumai has done the work - Next post I will fill the gaps and give the solution in formal way)
One of the great mathematician I admire is Madhava from Kerala, who did his work centuries before Newton (in 1300-1400). Some of the books written by his students and other people from that Kerala school were taken to Europe and has influenced many mathematicians. Among such work is series expansion of sin, cos, etc - centuries before Taylor, Newton, Libenitz or Gregory. Only in last few decades, these are now known as Madhava series - (When I was in school, the text books did not give credit to Madhava -- only current books call them "Madhava series" (or Madhava-Newton or Madhava-Gregory etc).
Any way where π comes in this problem, is from the famous Madhava series (also called Gregory series in old textbooks). Here is a cut and paste from Wiki: ( see Madhava Series
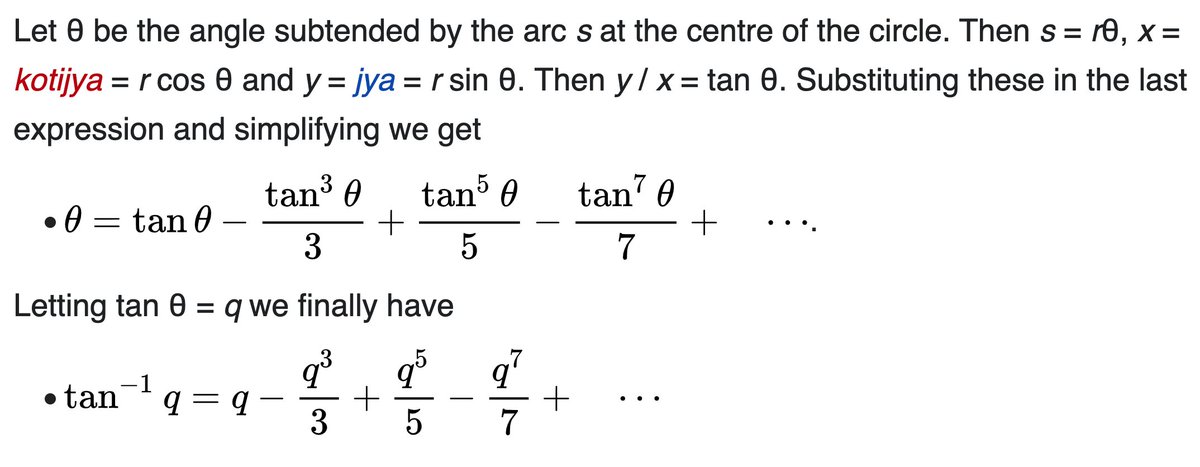
If you substitute θ = π/4
You get π/4 = 1 -1/3 + 1/5 - 1/7 + 1/9 - ....
This is beautiful as on RHS you see just plain odd numbers, and LHS you see Pi...
(This, and similar series can be used to calculate Pi - In late 60's when I got my hands on a computer - IIT Kanpur (probably than the only computer in an academic school in India) - I used a similar series to calculate pi up to few hundred places of decimals)
****
The above problem can be reduced to this series.
Last edited by Amber G. on 18 May 2020 23:16, edited 1 time in total.
Re: BR Maths Corner-1
Okay - Here are the basic steps -- starting with:
2. One can write (1/(n(n+1)) as 1/n - 1/(n+1)
3. If the numerator was always "+" can you sum the series ... (Hint: It is simple the answer is 2) (See note #1)
4 If the numerator's sign has pattern " - - + + - - + +" Can you sum the series (Answer is 2-Pi) (see note #2)
Note #1:
In this case: The series given in this case becomes (if all signs are positives) 2 (1 - 1/2 + 1/2 - 1/3 + 1/3 - 1/4 .... ) = 2 as (-1/2 and +1/2 cancels out etc..)
Note #2:
The series (the one asked in the problem) becomes:
2 (-(1-1/2) - (1/2-1/3)+ (1/3-1/4) + (1/4 - 1/5) - (1/5-1/6) - (1/6 - 1/7) ....
= -2 + 4/3 - 4/5 + 4/7 - ...... ( Terms with even denominator cancels out while the one's with odd ones chances sign etc..)
= 2 - 4 (1 - 1/3 + 1/5 - 1/7 ...)
which is nothing but (2 - π ) , if you use the Madhava series in the previous post!
1. The pattern of "signs" of each term in above goes as " -1, -1, +1, +1, -1, -1, +1, +1 " ...Looking at the expression as 2*i^(n*(n-1))/(n*(n-1)) seemed promising but couldn't take it further.
2. One can write (1/(n(n+1)) as 1/n - 1/(n+1)
3. If the numerator was always "+" can you sum the series ... (Hint: It is simple the answer is 2) (See note #1)
4 If the numerator's sign has pattern " - - + + - - + +" Can you sum the series (Answer is 2-Pi) (see note #2)
Note #1:
In this case: The series given in this case becomes (if all signs are positives) 2 (1 - 1/2 + 1/2 - 1/3 + 1/3 - 1/4 .... ) = 2 as (-1/2 and +1/2 cancels out etc..)
Note #2:
The series (the one asked in the problem) becomes:
2 (-(1-1/2) - (1/2-1/3)+ (1/3-1/4) + (1/4 - 1/5) - (1/5-1/6) - (1/6 - 1/7) ....
= -2 + 4/3 - 4/5 + 4/7 - ...... ( Terms with even denominator cancels out while the one's with odd ones chances sign etc..)
= 2 - 4 (1 - 1/3 + 1/5 - 1/7 ...)
which is nothing but (2 - π ) , if you use the Madhava series in the previous post!
Re: BR Maths Corner-1
Just got the Children's book "The Boy who dreamed of Infinity" (about Ramanujan) written by daughter of the G. Andrews (who found the "lost" notebooks of Ramanujan) - Read it before giving it to the children .,Liked it.
Re: BR Maths Corner-1
Just for fun:
Two problems, if you like to find any elegant methods to solve, or to challenge others:
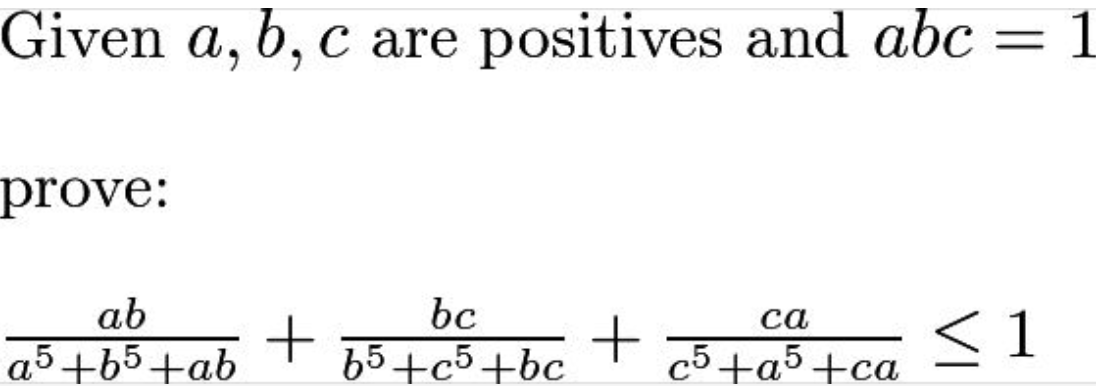
Somewhat harder: For number theorists (or computer programmers)
Sum of the first 'y' natural numbers = Sum of the squares of the first 'x' natural numbers.
Are there any solutions (in positive integers) other than x=y=1?
If so how many?
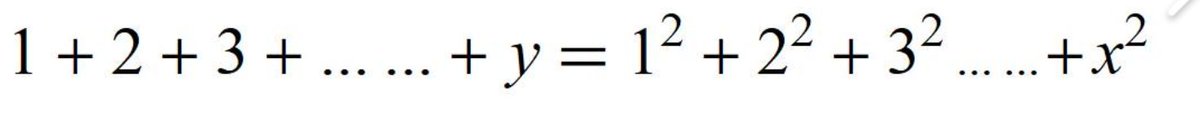
Two problems, if you like to find any elegant methods to solve, or to challenge others:
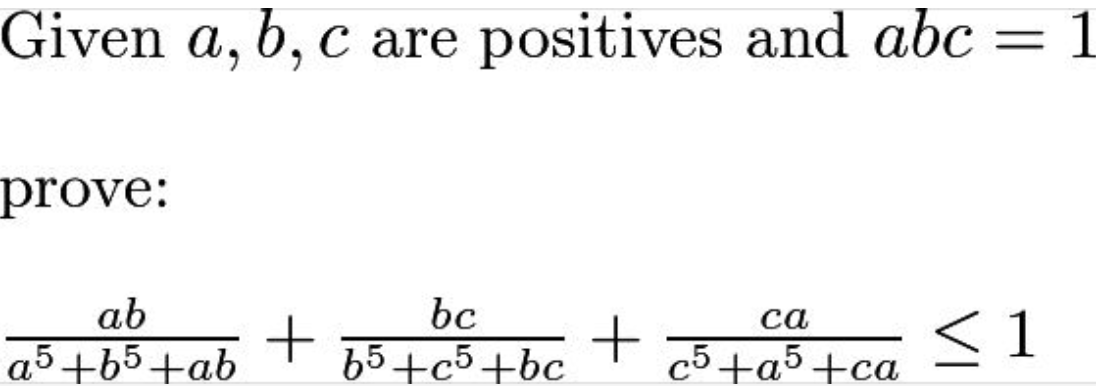
Somewhat harder: For number theorists (or computer programmers)
Sum of the first 'y' natural numbers = Sum of the squares of the first 'x' natural numbers.
Are there any solutions (in positive integers) other than x=y=1?
If so how many?
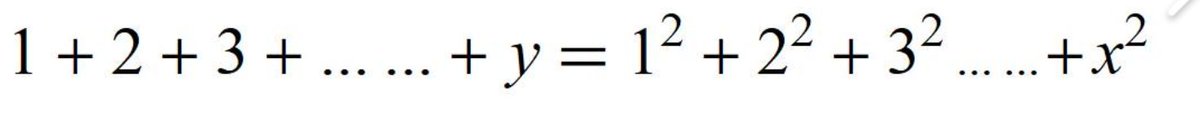
Re: BR Maths Corner-1
Here is a small article I wrote on Mathematics, Indian music and Poetry and partitions for my personal amusement. I gave proofs of all statements.
https://sites.math.rutgers.edu/~chanillo/music.pdf
%%%%%%%
The original notes on Number Theory has experienced a tremendous change. Some of the highlights in this now final version:
1. A proof of a special case of Jacobi's theorem by just High scholl method and a short proof. The original proof of Jacobi uses deep identities for theta functions. It would be spectacular to prove the full Jacobi theorem using the simple high school method of the notes.
2. A proof of the famous Dirichlet theorem on averages of divisors. I even take it further and prove Voronoi's theorem that is taking to almost the state of the art and now you are in conjecture territory. To improve Voronoi is I think very hard and needs a new idea. But you can see where the difficulty is. Uses Fourier series.
3. A proof of the Rabinovitch theorem of prime spitting polynomials. This is deceptive, the proof looks short less than 2 pages, but employs some machinery in algebraic Number theory.
4. A simple proof of Gauss's reduction theorem, elementary.
There is very little original research here except I have taken pains to present the material in a clear fashion keeping in mind future developments.
https://sites.math.rutgers.edu/~chanill ... number.pdf
https://sites.math.rutgers.edu/~chanillo/music.pdf
%%%%%%%
The original notes on Number Theory has experienced a tremendous change. Some of the highlights in this now final version:
1. A proof of a special case of Jacobi's theorem by just High scholl method and a short proof. The original proof of Jacobi uses deep identities for theta functions. It would be spectacular to prove the full Jacobi theorem using the simple high school method of the notes.
2. A proof of the famous Dirichlet theorem on averages of divisors. I even take it further and prove Voronoi's theorem that is taking to almost the state of the art and now you are in conjecture territory. To improve Voronoi is I think very hard and needs a new idea. But you can see where the difficulty is. Uses Fourier series.
3. A proof of the Rabinovitch theorem of prime spitting polynomials. This is deceptive, the proof looks short less than 2 pages, but employs some machinery in algebraic Number theory.
4. A simple proof of Gauss's reduction theorem, elementary.
There is very little original research here except I have taken pains to present the material in a clear fashion keeping in mind future developments.
https://sites.math.rutgers.edu/~chanill ... number.pdf
Re: BR Maths Corner-1
@vsunder ji, thanks once more. I downloaded and updated the previous version.