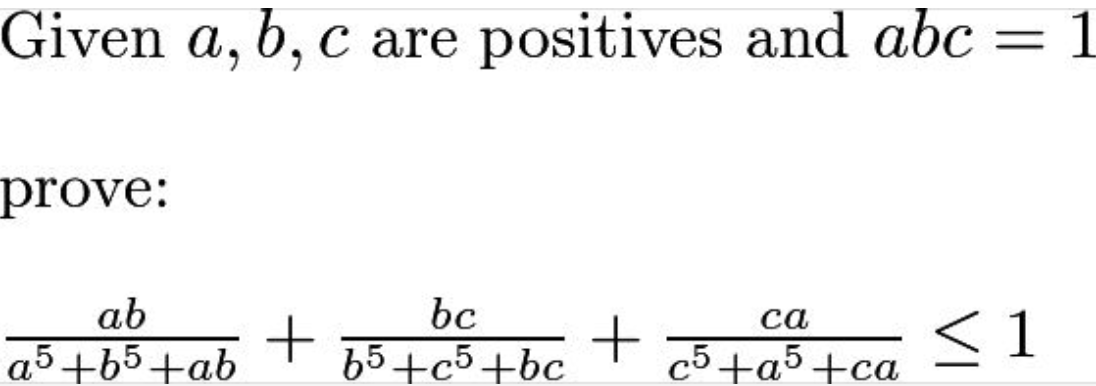sudarshan wrote:The second problem (easier version) reduces to finding all positive numbers "a" such that:
2*a^2+1 is a perfect square
(OR)
2*a^2-1 is a perfect square
For any such a:
for the first case, y=2*a^2, x=a*sqrt(2*a^2+1)
for the second case, y=2*a^2-1, x=a*sqrt(2*a^2-1)
Now if only I knew how to find all those "a" values in a general way.
<The pattern (0.0)(1,1),(6,8),(35,49)(204,288) .... etc...>
But why is this pattern this way?
Excellent!
Now the pattern, say for x is given by x_n = 6*x_(n-1) - x_(n-2)
In other words, if first value of x=0, and second value = 1 , then the
next one is
6*1 - 0 =6
Next value is
6*6 -1 = 35
Next one is
6*35 - 6 = 204
Next one is
6*204 - 35 etc....
And so on..
(This is not hard to prove, and I will show it fairly soon later in the post - proof can be seen in any good book too - look up "Pell's equation" (the correct name ought to be Brhamgupta equation) also there are problems here in Brf dhaga similar to this where the proof is given ).
----
The interesting anecdote - some one asked Ramanujan a similar problem while he was taking a walk - Ramanujan, of course, answered it immediately. The answer was many digits long yet he answered it almost right-away- without even a paper or pen. His friend was really surprised (his friend was also quite a good Indian mathematician who was also studying in Cambridge and heard that problem) to see this. He asked how did Ramanujan do it so quickly - (The standard method using Pell's equation does require more than a few seconds) .. Ramanujan answered - " He knew the answer is related to continued fraction of sqrt(2).
Now sqrt(2) = 1 / (2+1 /( 2+ 1/ + ---) or:
<see graphics here>or wiki for article on continued fraction. (eg:
https://en.wikipedia.org/wiki/Square_ro ... esentation
Or IOW: the approximation for sqrt(2) by expanding this continued fraction, you get the fractions ..
are
1/1, 3/2, 7/5, 17/12, 41/29, 99/50 ....
Each fraction in the series is a better approx of sqrt(s)
Now if you multiplied denominator and numerator (eg 3*2=6, 7*5=35, 17*12 you get successive values of x)
So above is the continued fraction method.
(Intuitively - as Ramanujan will say . you if you want 2*a^2 +-1 = b^2 the ratio of b and a is nearly sqrt(2)..so if working with integers, the continued fraction of sqrt(2) is the way to go).
****
Now if you want explicit formula here choose any integer n
x = ((3+2 √ 2)^n - (3 - 2 √ 2)^n) / (4 √ 2)
y = ((3+2 √ 2) ^n + (3 - 2 √ 2) ^n - 2)/ 4
It's easy to put in the computer, (easy to verify that x and y both are integers and has the required property).
****
Hope people find it fun,