BR Maths Corner-1

[Amber G.]

Best of luck:
(IMO - International Math Olympiad is most important/prestigious international contest)
Indian team for IMO 2024
Adhitya Mangudy - Bronze at IMO 2023
Ananda Bhaduri - Silver at IMO 2023
Arjun Gupta Gold at IMO 2023
Kanav Talwar - first attempt
Rushil Mathur - first attempt
Siddharth Choppara Silver at IMO 2023

USA Team

Jordan Lefkowitz
Krishna Pothapragada
Linus Tang
Jessica Wan
Alexander Wang
Qiao Zhang

[Amber G.]

^^^ The International Mathematical Olympiad (IMO) is taking place this week in Bath, UK (originally scheduled for Kiev, Ukraine). The two 4.5-hour exams are on Tuesday and Wednesday, with results to follow in a few days. The closing ceremony is on July 21, 2024. As usual, I'm excited to review the problems this year. (As usual, will get to day's problems after the exam is over and students can share the problems).

Another very interesting aspect for me:

The 2024 IMO features a $10 million AIMO Prize for an AI to win an IMO gold medal, technical advised is Po-Shen Loh (prof at CMU - IMO gold medalist, known/mentored him (and his family - all *very* accomplished mathematicians) since he was in high-school ). Google Deep Mind and AlphaGeometry are participating, making this a thrilling math + AI showdown! It's exciting to see how the world's brightest high school students will fare against the latest AI systems.

Notably, even Terry Tao (Field Medalist and one of the top mathematician in the world) is enthusiastic about the integration of AI systems into research mathematics and is encouraging the community to embrace this disruption.

[Amber G.]

^^^ Here is one of the easier one from today:

Find all real number x such that for any positive integer n
⌊x⌋+ ⌊2x⌋+ ⌊3x⌋+⌊4x⌋ ....⌊n x⌋ is a multiple of n

Note that floor function is used .. ⌊x⌋ means integer part (for positive values of x)... eg
⌊2.15⌋ = 2, ⌊2.9⌋=2 , ⌊-2.15 ⌋ = -3

(Hint Problem is looks very easy to describe and not vary hard)

[Vayutuvan]

Talking of Pen-Sho Loh, here is a nice article on a new short and sweet method of solving quadratic questions in single variable.

https://arxiv.org/pdf/1910.06709

[Submitted on 13 Oct 2019 (v1), last revised 16 Dec 2019 (this version, v2)]
A Simple Proof of the Quadratic Formula
Po-Shen Loh
This article provides a simple proof of the quadratic formula, which also produces an efficient and natural method for solving general quadratic equations. The derivation is computationally light and conceptually natural, and has the potential to demystify quadratic equations for students worldwide.

Comments: 8 pages
Subjects: History and Overview (math.HO)
Cite as: arXiv:1910.06709 [math.HO]

[sudarshan]

^^^ Here is one of the easier one from today:

Find all real number x such that for any positive integer n
⌊x⌋+ ⌊2x⌋+ ⌊3x⌋+⌊4x⌋ ....⌊n x⌋ is a multiple of n

Note that floor function is used .. ⌊x⌋ means integer part (for positive values of x)... eg
⌊2.15⌋ = 2, ⌊2.9⌋=2 , ⌊-2.15 ⌋ = -3

(Hint Problem is looks very easy to describe and not vary hard)

[Amber G.]

^^^ Nice one!
(May be BRF should enable LaTex in the forum. .)

[Amber G.]

Interesting tidbit -- From Australia's team 4 ( out of 6 ) are girls... 2 of them are twin sisters.
(Very rare.. as most countries there are very few girls in the team)..

(Australia boast Olympians like Fields Medallist Terence Tao, and Grigori Perelman who famously solved the Poincaré conjecture then rejected the million dollar prize)

From what I know, in USA Melanie Wood (represented the US in the 1998 and 1999 IMO and won Silver Medals in both years. She was the first female to qualify for the IMO from the United States.), Alison Miller:( Gold 2004 ) and Sherry Gong (2005 and 2007, Gold in 2007) are the only females.
(Proud to know/interacted /mentored Melanie and Alison ).

(Indian teams have more girls ( about 8 or so) especially lately.)

[Amber G.]

Allow me to post Problem 2 -- (I liked it, it is nice application of FLT theorem -- which I mentioned in this math dhaga many times) ..idea and problem is from Indonesian mathematician,

Determine all pairs (a, b) of positive integers for which there exist positive integers g and N such that
𝑔𝑐𝑑(𝑎ⁿ+𝑏,𝑏ⁿ+𝑎)=𝑔

holds for all integers n ⩾ N.
(Note that gcd(x,y) denotes the greatest common divisor of integers x
and y.)

(Basically it means, find all such pairs of natural numbers (a,b) such that 𝑔𝑐𝑑(𝑎ⁿ+𝑏,𝑏ⁿ+𝑎) remains (some) finite (values) no matter how big n becomes.)

For example a=b=1 the gcd is 2 (𝑎ⁿ+𝑏= 1^1+1=2) is one solution.

--- All the problems are now on the IMO website

[Amber G.]

Another fun problem:

Turbo the snail plays a game on a board with 2024 rows and 2023 columns. There are hidden monsters in 2022 of the cells. Initially, Turbo does not know where any of the monsters are, but he knows that there is exactly one monster in each row except the first row and the last row, and that each column contains at most one monster.
Turbo makes a series of attempts to go from the first row to the last row. On each attempt, he chooses to start on any cell in the first row, then repeatedly moves to an adjacent cell sharing a common side. (He is allowed to return to a previously visited cell.) If he reaches a cell with a monster, his attempt ends and he is transported back to the first row to start a new attempt. The monsters do not move, and Turbo remembers whether or not each cell he has visited contains a monster. If he reaches any cell in the last row, his attempt ends and the game is over.
Determine the minimum value of n for which Turbo has a strategy that guarantees reaching the last row on the nth attempt or earlier, regardless of the locations of the monsters.

[sudarshan]

Another fun problem:

Turbo the snail plays a game on a board with 2024 rows and 2023 columns. ...

I found this one to be easy (hope I didn't mess up) - is there anybody at the Olympiad who did NOT solve it?

It also seems the solution is independent of the number of rows, columns, and monsters, so long as number of rows=N, number of columns=N-1, and number of monsters=N-2 with all the other conditions being the same.

I showed the solution with 11 rows, 10 columns, 9 monsters. Same principle for any other N, N-1, N-2 row/ column/ monster set-up.

[Amber G.]

^^^This problem is indeed *very* easy, ( my 8 year grandson solved it).. Don't know the whole story now but I suspect it is somebody's mistake/stunt or such thing.. Problem is too easy for IMO level..
(Unless I missing some thing).
(BTW. The graphics in your post is beautiful .. i hope it is okay with you if I borrow it )

[sudarshan]

^^^This problem is indeed *very* easy, ( my 8 year grandson solved it).. Don't know the whole story now but I suspect it is somebody's mistake/stunt or such thing.. Problem is too easy for IMO level..
(Unless I missing some thing).
(BTW. The graphics in your post is beautiful .. i hope it is okay with you if I borrow it )

Sure, you can borrow the graphics.

I saw the solution as - find any one monster as fast as possible, then find a way to get under it, as that guarantees a clear path to the bottom. So then the best monster to find would be the one in the second row, as that takes the least number of attempts (just one).

But getting under a monster is the most difficult, when the monsters are arranged diagonally and one is on the "wrong side" of the diagonal. So then I thought - why not move diagonally to begin with, and see what happens? And that worked.

[Amber G.]

^^^ Thanks. Nice solution and graphics.

My guess was right. The problem has already become famous for the not only the longest word problem in the history of IMO but also the most "trolled" problem.. Came to know the back story how this problem made it to IMO.... (I would like to see the individual results). ..

[Amber G.]

The IMO site has nothing posted as results ...The final jury meeting is tomorrow .( so final medals will be officially decided tomorrow) . but it seems that India has done extremely good! (Looks like it is in the 3rd or 4th place!! - First time.. behind USA and China .. but ahead of powerhouse like Russia etc..)...(I think it has total 176 points)

(Will post medal counts etc .. when it is official ... let us see how long it makes main-stream news in India)

(BTW Sudarshan for problem you said (P5).. 5 out of 6 people in India got full scores )

*** Added later, from the latest (unconfirmed / not official but quite sure)
Cutoff for medals is decided (16/22/29) ... this means India has 5 golds and 1 bronze .. (Official 4 gold 1 silver) and the results Top 4 are 1st-USA, 2nd-China 3rd- 4 th - India and one (CHN-4 ) scored perfect score!
Congrats to India - First time it is in top 5!
Jai Hind
(I will correct it/edit it when results are posted or official)

[Amber G.]

Final scores of IMO 2024 are:

1 - United States of America - (192 5- Gold 1 - silver)
2- People's Republic of China - ( 190 5 - Gold 1 - Silver)
3- Republic of Korea (168 2 Gold 4 Silver)
4- Bharat (India) ( 167 4 Gold 1 Silver 1 HM )
5 - Belarus (165)
6 - Singapore (162)
7 - United Kingdom (162)
8 - Hungary (155)
9 - Poland (151 )
10 - Türkiye

Jai Hind!

Congratulations to India and USA ! ( Both in top 5 - for the first time)

(I corrected my previous post(s) -- based on the latest scores available -- India' lost a position by just 1 point. It lost 1 gold and 1 silver by just 1 point to -- not that it matters!)


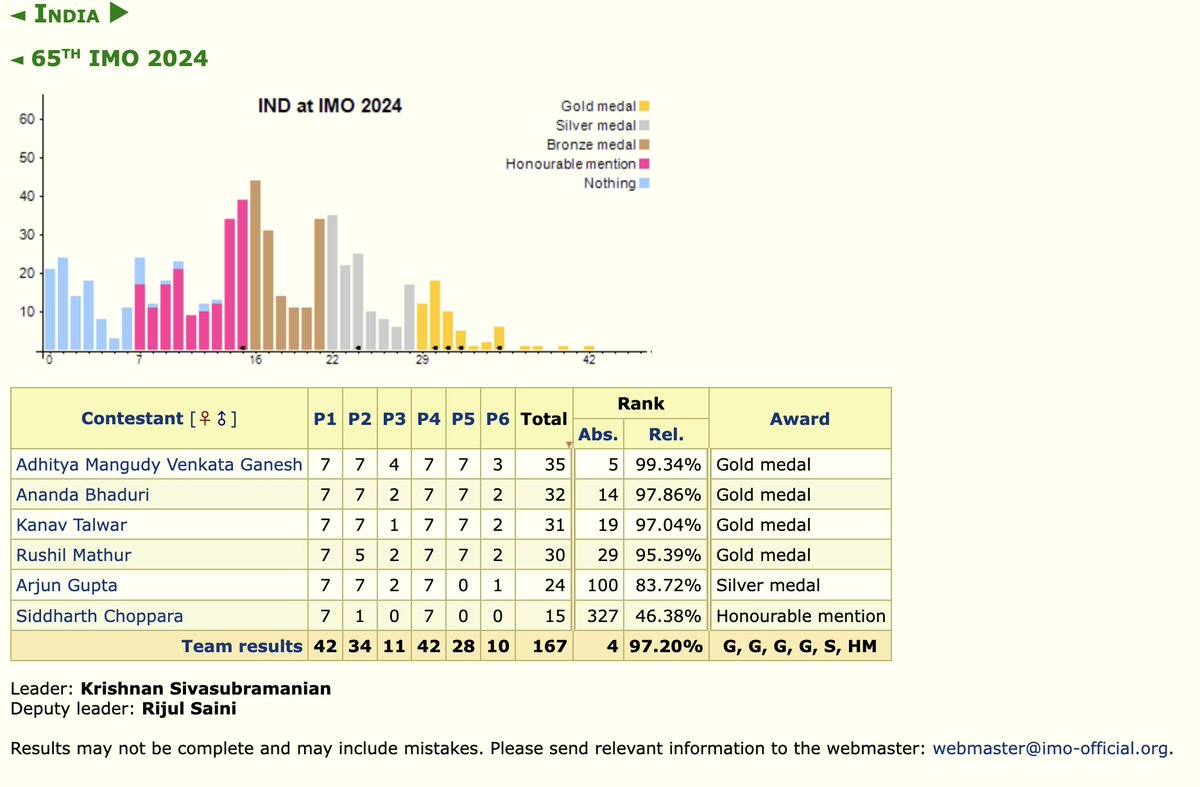
(I also incorrectly guessed the Problem 5 scores ..-- thought everyone will solve it )

[saip]

The US team winners: Wang, Wan, Tang, Pothapragada, Zhang and Lefkowitz!
This could pass for a Chinese team except for the lone Indian and a Pole!

[Amber G.]

I found this one to be easy (hope I didn't mess up) - is there anybody at the Olympiad who did NOT solve it?

I tried some AI -- did not do good in the math part but it liked the picture..
(Along with Sudershan's solution this picture can go along )


---

Just did a google search -- STILL NO NEWS in any of Indian News Papers!
( I have this in my social media -- which some news reporters (mainly in science) follow -- but still the news have not been picked up ... will be i interesting to see how long does it take.. for Indian Papers to pick up the news)
-- (I am going to send it to few sources to see if anyone picks it up)

[sudarshan]

I was able to show that (with a<b) a would necessarily have to be 3, and b would necessarily have to be 5, to provide a non-trivial solution for the ghee-chaddee problem. However, I wasn't able to prove sufficiency.

I saw the note saying "interesting application of FLT" so went and looked up FLT. Search said "Fermat's Last Theorem" so I got stuck on that, before I realized there was another FLT - "Fermat's Little Theorem." How confusing.

So I put together a brew using FLT, then let it Fermat (I mean - ferment), and came up with the below.

[sudarshan]

Oh - logic got messed up at one particular point in the above. Solution not totally valid, will retry.

[Amber G.]

^^^ Have not had time to look in details:
- But FLT is indeed Fermat's Little Theorem ( Our son when he was little called it "Little Fermat's Theorem" - so that name is some times used by me )..
(It is seldom taught in high-school or even in undergraduate level math in India - but can be easily understood in school is it very nice --- but *very* few people in a typical school are familiar with it)

-

[Vayutuvan]

FST: Fermat’s Small Theorem (?) now that F’s “last theorem” conjecture is proved, i.e. a theorem.

[Amber G.]

As I said (in another dhaga and some of my SM posts)... none of the mainstream media in India picked up the news... so I was surprised and sent a message to some newspapers and few people in Modi government and academia... . Well somebody did notice!

Final scores of IMO 2024 are:

1 - United States of America - (192 5- Gold 1 - silver)
2- People's Republic of China - ( 190 5 - Gold 1 - Silver)
3- Republic of Korea (168 2 Gold 4 Silver)
4- Bharat (India) ( 167 4 Gold 1 Silver 1 HM )
5 - Belarus (165)
6 - Singapore (162)
7 - United Kingdom (162)
8 - Hungary (155)
9 - Poland (151 )
10 - Türkiye

Jai Hind!

Congratulations to India and USA ! ( Both in top 5 - for the first time)

(I corrected my previous post(s) -- based on the latest scores available -- India' lost a position by just 1 point. It lost 1 gold and 1 silver by just 1 point to -- not that it matters!)


(I also incorrectly guessed the Problem 5 scores ..-- thought everyone will solve it )

[Amber G.]

Now.. (after some time) the news is getting in the mainstream India..
PM Modi applauds India's record performance in Maths Olympiad 2024

[Amber G.]

From left to right: Mainak, Arjun, Adhitya, Rushil, Siddharth, Kanav, Ananda, Rijul
The 6 student winners are Adhitya, Ananda, Kanav, Rushil (Gold), Arjun (Silver), Siddharth (HM)
Leaders: Krishnan Sivasubramanian, and Rijul Saini,
Observers: Rohan Goyal and Mainak Ghosh
(Picture Credit - TIFR/HBCSE)

[Amber G.]

The Winners are back! The Indian Team to the 2024 International Mathematics Olympiad returned to HBCSE this morning & were felicitated by Dr Ajit Mohanty Chair AEC and Secr @ DAEI
4 Golds, 1 Silver, & 1 Hon Mention, this was India's best performance till date at the IMO.

[ramana]

Intl Math Olympiad questions

https://x.com/deedydas/status/181489114 ... tYQpA&s=19

[Amber G.]

^^^ Thanks.
Also as usual they are posted on the official site. (Not only 2024 but all the previous contests, as mentioned here before).

The link is https://www.imo-official.org/problems.aspx

There 'official solutions' are also on the uk's IMO2024 official site (https://www.imo2024.uk/)

-----

This year's IMO (In my Opinion) there were 4 relatively easy questions in IMO (International Maths Olympiad) - I could get it literally within few minutes (and my son/grandson - similarly). Funny thing P5 (discussed above) is now known as "troll' type problem - very easy but people may get confused not to try it). From HK. Sudarshan has neat solution here..of both P5 and P1.
(If there is interest - i can give simple solutions for other two which can be understood by elementary level math )

[Amber G.]

Modi interacts with winners of International Mathematical Olympiad

[Amber G.]

Nice Video Message:
From PM:मेरा सभी देशवासियों से आग्रह है कि Paris Olympics में हिस्सा ले रही भारतीय टीम का उत्साह जरूर बढ़ाएं। इसके साथ ही International Mathematics Olympiad में देश का मान बढ़ाने वाले हमारे युवा महारथियों को भी बहुत-बहुत बधाई।

[Amber G.]

^^^ Small tidbit : In this years IMO contest, I think females were about 10%..
But from Australia (Famous IMO Gold Medallists include Australian Fields Medallist Terence Tao, and Grigori Perelman in the past) There were 4 of the 6 contestants were females!

(Laura Nan, Amber Li, Cloris Xu, Iris Xu -- Cloris and Iris are twins - Picture Credit- ( Australian Maths Trust)

[Amber G.]

Talking of Pen-Sho Loh, here is a nice article on a new short and sweet method of solving quadratic questions in single variable.

Allow me to share a nice article about Po-Shen Loh - (somebody I knew when he was in high-school competing for math contests)...He was IMO coach of US team ..Many students from India were also helped.
The Coach Who Led the U.S. Math Team Back to the Top

He shares his recent experience with AI and IMO type questions (there was a $10 million dollar prize for any AI - if it can get a gold medal at the olympiad - AI was not able to win that medal)
For the detail see NY times article .https://www.nytimes.com/2024/07/25/scie ... pmind.html

[Amber G.]

Just for fun..here is one easy one..

[sudarshan]

Just for fun..here is one easy one..
....

The answer has got to be 2.4. Here's the reasoning:

Let the numbers be a, b, c, d.

Obviously none of them are zero, since that would lead to multiple zeros in the pairwise products. But the pairwise products are 2, 3, 4, 5, 6, and x.

If one of a, b, c, d is negative, that would lead to three negatives in the pairwise products.

If two of a, b, c, d are negative, that would lead to 4 negatives in the pairwise products.

If three of a, b, c, d are negative, that would lead to 3 negatives in the pairwise products.

Thus, either all of a, b, c, d are negative, or all of them are positive.

If any two of a, b, c, d are the same number, that would lead to 4 of the pairwise products being the same.

If any three of a, b, c, d are the same number, that would lead to at least 3 of the pairwise products being the same.

If all four are the same number, then obviously all the pairwise products would be the same. So a, b, c, d are distinct numbers.

Then we can order them as a < b < c < d. For positive a, b, c, d (the case where all of them are negative would simply be the same as the positive case, but with negative signs):

The pairwise products (PWPs) are ab, ac, ad, bc, bd, cd.

These PWPs would then necessarily have to be in the order:

ab < ac < (either ad or bc) < (either ad or bc) < bd < cd.

Now: ab * cd = ac * bd = ad * bc ---------------------------- (1)

Thus, if we take the PWPs 2, 3, 4, 5, 6, x - we need to be able to group them into three groups of 2 each, such that the product of each group is the same value.

Depending on the value of x, we can have:

x < 2 < 3 < 4 < 5 < 6; 2 < x < 3 < 4 < 5 < 6; 2 < 3 < x < 4 < 5 < 6; 2 < 3 < 4 < x < 5 < 6; 2 < 3 < 4 < 5 < x < 6; 2 < 3 < 4 < 5 < 6 < x

Using equation (1), for the above cases, we would have:

x * 6 = 2 * 5 = 3 * 4 -------- (impossible)
2 * 6 = x * 5 = 3 * 4 -------- (leads to x being 2.4)
2 * 6 = 3 * 5 = x * 4 -------- (impossible)
2 * 6 = 3 * 5 = 4 * x -------- (impossible)
2 * 6 = 3 * x = 4 * 5 -------- (impossible)
2 * x = 3 * 6 = 4 * 5 -------- (impossible)

Thus, x has to be 2.4. One can solve for two cases with this value of x:

ab = 2; ac = 2.4; ad = 3; bc = 4; bd = 5; cd = 6 (or) ab = 2; ac = 2.4; bc = 3; ad = 4; bd = 5; cd = 6

For the first case:

a = sqrt(6/5), b = sqrt(10/3), c = 1.2 * b, d = 2.5 * a

For the second case:

a = sqrt(8/5), b = sqrt(5/2), c = 1.2 * b, d = 2.5 * a

Obviously, the cases where

a=-sqrt(6/5), b = -sqrt(10/3), c = 1.2 * b, d = 2.5 * a

and

a = -sqrt(8/5), b = -sqrt(5/2), c = 1.2 * b, d = 2.5 * a

will also work.

In all these cases, the unknown sixth pairwise product is x = 2.4.

[Vayutuvan]

One can eliminate <math>\mathbb{N}</math> solution because 2, 3, and 5 are primes. Then the fourth number has to be 1. Then 4 is not a product of any pair.
Shorter proof is possible (?) if we assume the solution is in <math>\mathbb{Q}</math>?

<math>12/5 \in \mathbb{Q} </math>

[Amber G.]

One can eliminate <math>\mathbb{N}</math> solution because 2, 3, and 5 are primes. Then the fourth number has to be 1. Then 4 is not a product of any pair.
Shorter proof is possible (?) if we assume the solution is in <math>\mathbb{Q}</math>?

<math>12/5 \in \mathbb{Q} </math>

Sorry but IMO quite sloppy ( and unhelpful ) logic..Absurd to assume to draw conclusions like .. something based on some numbers being "prime". (Since NO ONE has told that the numbers are integer etc) ... product of two numbers can be 5 while none of the number is one.. (eg 4* (5/4) = 5)..

The problem is *really* for elementary school person, familiar with fractions etc.. slight unusual but quite easy..(and straight forward).

(Hint: Once you notice that 6*2=4*3=12 ... the missing product 12=5*(12/5)...)
(Three set of these "products" of (two products values) will result into (ab)(cd) = unique number)

As pointed out excellently by Sudarshanji :

Now: ab * cd = ac * bd = ad * bc ---------------------------- (1)

/smile/

[Vayutuvan]

Sorry but IMO quite sloppy ( and unhelpful ) logic..Absurd to assume to draw conclusions like .. something based on some numbers being "prime". (Since NO ONE has told that the numbers are integer etc) ... product of two numbers can be 5 while none of the number is one.. (eg 4* (5/4) = 5)..

This is ridiculous. I am not smarter than a gifted elementary school kid.

Humility, my friend, humility. It helps everyone go a lot further.

You want to directly go to real field but that was not how mathematics developed.

I put it to you the following.

1. You study mathematics once as axioms, examples, lemmas, theorems.
2. You study math a second time the way it developed over a period of time.

If you don't do the second part, you would not be able to differentiate between a deep result and an elementary school exercise.

IMO, Putnam, or some other competition, child prodigy in Chess/Number Theory or what have you, is not really that important when you have to deal with the real problems or abstract mathematics.

(I am being sloppy in my terminology below as this is a casual discussion)

There are a certain number of "tricks" in the toolbox of a mathematician. One needs to know all the tricks and apply them to solve new problems. But just that won't be enough. One needs to develop new "tricks" to solve new problems and/or shorter proofs for old theorems and conjectures as well as to find connections (deep ones) between totally different fields of mathematics.

Solving puzzles is good at lower levels, but it is neither necessary nor sufficient for someone to be able to create new mathematics.

I am speaking as a Theoretical Computer Scientist and practicing applied mathematician.

[Vayutuvan]

My advisor is a very highly regarded Computer Scientist by Fan Chung when they were in the same research group at a now defunct research lab. I am very much influenced by his way of working and his way of looking at problems.

[Vayutuvan]

Teaching is not highly regarded now a days. Only research (getting grants and writing papers - publish or perish) used to get tenures. Even that is not the case anymore, not in CS at least. Even in 90s the joke was "publish still perish".

Even as late as 1970s it, was possible to get an TT position with no PhD. Today one cannot get a TT even at a community college without a PhD or a lot of experience. In research labs, MS folks are treated as second tier. I am not saying it is right. But that what it is.

It is impossible to get an academic position in any ares of Physics or Chemistry unless you are at a genious level person with academic pedigree. All this training for IMO, Physics/Chemistry olympics is very similar to training for Olympics.

What is going to happen to the majority of the non-medal winning participants people (by definition they are the majority) later on?!

In academics, they can at least change their field to engineering, technology, or applied sciences (drug research) but athletics is dead end, just like Music, Chess, high arts, etc.

Even in the US, opportunities have dried up for "pure" mathematics (if there was ever such a beast).

Hilbert and one of the most famous students, Courant both were applied mathematicians. Courant is famous for starting Applied Math department at NYU.

Solving some one off problems is just a game like playing a game of chess or go or solving an instance of sudoku. In the larger scheme of "pushing the envelope", creating new mathematics, novel applications in engineering/public health solutions/improving human life, these are of little importance.

This is not to pour cold water on enthusiasm, wonder, and curiosity. But at some point, people have to grow out of this immaturity of getting excited at every small advance that physics community makes or every small theorem that some cryptographic researcher proves or a new NT based algorithm which is the new shiny thang.

[Amber G.]

Ramnujan Inspires Gold Medal and world Record in Paris Olympics!

I have written about my friend Prof Ken Ono - one of the world leading authority about Ramnujan's work in Math dhaga many times.

Ken Ono, a world-renowned mathematician, has made significant contributions to the field of number theory. He was an advisor for the film "The Man Who Knew Infinity," which tells the story of Srinivasa Ramanujan's life and work. Ono's expertise also extends beyond academia; he helped Olympic gold medalist Kate Douglass optimize her performance in the 200m breaststroke, (World record) using mathematical techniques to analyze and improve her technique. Douglass, who holds the American record in the event, credits Ono's insights for her success. Ono's unique ability to apply mathematical concepts to real-world problems has made him a sought-after collaborator across disciplines.

Picture Credit: Prof Ono

[S_Madhukar]

He shares his recent experience with AI and IMO type questions (there was a $10 million dollar prize for any AI - if it can get a gold medal at the olympiad - AI was not able to win that medal)
For the detail see NY times article .https://www.nytimes.com/2024/07/25/scie ... pmind.html

A similar talk Tao gave explaining how chatGPT like agents say Lean CoPilot can help in maths formalisation thus saving time, moderated by Loh -

https://youtu.be/_sTDSO74D8Q?si=o2Z6Y_QspTqr9-B6