For the second one, intuitively, the answer is:
squareroot(( det (A(transpose)*A))
Of course. What was I thinking. The sign of det(A) gives the sign of the area.Amber G. wrote:SKM - Not to nit-pick but "sqr(A)" (actually the "root" sign) (by accepted normal definition) means positive value onlee .. so "abs" in the second case need not be thre ... eg when one writes sqr(2) with either normal mathematical "root" sign or types it in google see here it means a (positive) number between 1.4 and 1.5 ..
Also, BTW (A(transose)*A) is always positive...so no need to put ABS there... (point is det(A) can be negative, but A(transpose)*A is always positive... (assuming of curse, as you said, you are dealing with real numbers)
I'm not really talking abt non-euclidean space. Just saying, no metric needs to be defined. You only need to define a measure. The normal volume measure can be obtained by taking a finite number (tending to infinity) of elementary cubes.Also - "volume(s)/areas" etc in non-Ecuadorian space(s) do have well defined meanings a little different .. (at least how normal mathematicians defines them) ...but I guess, it depends on the definition of "area" or "volume" so take it for FWIW..
except when it is zero.Amber G. wrote: Also, BTW (A(transose)*A) is always positive...
to which sk mody casually replied:Amber G wrote: Also, I will add "euclidean" in front of "n-dim" space
I need to qualify the statements I made.sk mody wrote: Just saying, no metric needs to be defined. You only need to define a measure. The normal volume measure can be obtained by taking a finite number (tending to infinity) of elementary cubes.
Should have used "non-negative"! (specially when I was busy last few days writing/editing "official solutions" to a regional math contestAlso, BTW (A(transose)*A) is always positive...
...except when it is zero. :
The point I was trying to make in response to your comment about euclidean metric, is that you do not need to impose a euclidean metric in order to define volume. You need to define a measure and not a metric. I later qualified that and said that if you need to define areas of lower dimensional subspaces in n-dimensional space - only then do you implicitly end up defining a metric.Amber G wrote: One can generalize classical meaning of "area" (or "volume") from 3 to n dimension ...It depends on how one defines/generalizes but for 2 (or 3) dimensional case, if we use formula's which we normally use for area/volume - they (or most formula's are valid) are valid for Euclidean space ... (hence, if you see wiki article, you may see qualifier 'Euclidean')
Problem: A goat is tied up with a rope of unit length. How much goat can roam? (or if there is grass - how much grass the goat can eat). (Goat is also restricted to move in a space of given dimension(s))
(pi ^ 2) / 6. This is the solution to the Basel Problem, and first solved by Leonhard Euler. Solving this brought him a lot of fame, since no one could solve it for over 100+ years.Amber G. wrote: what is the value of: (or what value this infinite series converge to?)
1+ 1/4 + 1/9 + 1/16 + 1/25 + 1/36 + 1/7^2+1/8^2 ...
goat eat grass pi*(1+dx)^2, no?Problem: A goat is tied up with a rope of unit length. How much goat can roam? (or if there is grass - how much grass the goat can eat). (Goat is also restricted to move in a space of given dimension(s))
If there are n dimensions the n-ball volume will be:Amber G. wrote:Problem: A goat is tied up with a rope of unit length. How much goat can roam? (or if there is grass - how much grass the goat can eat). (Goat is also restricted to move in a space of given dimension(s))
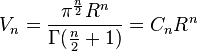
Yep! This some may find surprising ... the constant (C_n) increases in the beginning but after 5th dimension starts decreasing and becomes smaller and smaller as number of dimensions increase.Mohan G wrote:In the limit, as n->infinity, the n-ball volume shrinks to 0.
The answer is correct, of course. I find the result beautiful.ArmenT wrote:(pi ^ 2) / 6. This is the solution to the Basel Problem, and first solved by Leonhard Euler. Solving this brought him a lot of fame, since no one could solve it for over 100+ years.Amber G. wrote: what is the value of: (or what value this infinite series converge to?)
1+ 1/4 + 1/9 + 1/16 + 1/25 + 1/36 + 1/7^2+1/8^2 ...
Amber G. wrote: What are the first 100 digits after decimal point in the value of
(7+5 sqrt(2))^100 ?
ha! didn't read the full question.shaardula wrote:goat eat grass pi*(1+dx)^2, no?Problem: A goat is tied up with a rope of unit length. How much goat can roam? (or if there is grass - how much grass the goat can eat). (Goat is also restricted to move in a space of given dimension(s))
How that argument stands out for a smaller even integer, say x=2, or 4?ArmenT wrote:
I'm going to say 0.
Reason:
1. Forget all the integral numbers into the expression above because they don't play any part in the digits after the decimal point in the first place. The digits after the decimal point are really influenced by (sqrt(n))^X
2. If n is an integer and if X is even in step 1, then (sqrt(n))^X is an integer as well, since (sqrt(n))^X is the same as n^(X/2). Since X is even, X/2 is an integer. Since n is an integer, therefore it follows n^(X/2) is integer as well
3. Therefore first hundred digits after decimal point are 0.
Basically: All nondegenerate conics are projectively equivalent, so you might as well take (a unit) circle...
Okay?? I'm happy to be included in some sort of 'project' but exactly what have I done to deserve this honor? Then again, SHQ is firmly convinced about my loony streak, so perhaps you're a psychiatrist studying the levels of lunacy among BRF posters.shaardula wrote:amberg, thanks. i had not seen coffman. let me go through it.
Basically: All nondegenerate conics are projectively equivalent, so you might as well take (a unit) circle...it hear it is so too. but i dunno.

have a nice weekend. i have 2 'projects' for the weekend. one coffman another armenT.
Im a noob in this area and so, am assuming that if we can prove that the polynomial chosen for the LFSR is primitive, any random seed will ensure that the pattern will repeat only after (2^128 -1) outputs and all the outputs are completely random. Please confirm.The optimal LFSR is a primitive polynomial of GF(2), are you looking for a proof of this, or a method to check whether a particular polynomial is primitive? If I remember right (please check!), you need to prove that the polynomial divides x^(2^128-1)-1 .
One way would be to generate a large # of values and then apply a series of tests (chi-square, Kolmogorov-Smirnov, spectral test etc.) upon the set to see if they indicate any correlations. Donald Knuth ennumerates a series of tests in The Art of Computer Programming Vol II (sections 3.3.2 - 3.3.5 or so) that can be used to test randomness.sum wrote:Guys,
Does anyone know of a theorotical way of proving that the randomness of a LFSR with a base as a primitive polynomial of order,n=128 (with some random taps)?
This scientist realized that to create such a machine english was not useful. Math at it existed then, was definitely not useful. In his own wordsAnd now that we may give final praise to the machine; we may say that it will be desirable to all who are engaged in computations which, it is well known, are the managers of financial affairs, the administrators of others' estates, merchants, surveyors, geographers, navigators, astronomers. . . For it is unworthy of excellent men to lose hours like slaves in the labor of calculations.
Thus started a quest to define and discover (mathematical) logic. In case you wondered who this visionary mathematician was, it was Leibniz in circa 1680 !! Leibniz wanted a machine which could do calculation, based on a language that "perfectly captured the relationship between our thoughts" (a logical "program" as we call it today). Leibniz is regarded as the father of modern logic, he would write about 10,000 pages and not publish any. Because as he noted with sorrow, in one of the sheetsA script or language....that perfectly represents the relationship between our thoughts....how much better will it be to bring under mathematical laws, human reasoning, which is the most excellent and useful thing to have
This quest would last for centuries ! Tortuous progress would be made slowly. Martin Davis beautifully weaves history with funny and sad anecdotes, with individual triumph and loss, sadness and happiness with progress and setbacks in the field of mathematical logic. The reader gets to share the triumph of Boole, who realized if "true" is 1 and "false" is 0, if the "negation" of 1 were to be 0 and vice versa, if multiplication were regarded to be "AND", then the fact that a statement and its opposite cannot be true at the same time can be written as (negation of A) * A = 0. Which perfectly works out irrespective of whether A=0 or A=1. Thus Boolean logic was formed, which could capture, as algebra with purely symbolic operations some aspects of what we call as "logic". But Boole's logic was relegated as a curiosity in philosophy classes. Till Claude shannon noted that Boolean operators can be performed by electrical relays and voltage can be used to represent a 1 or a 0, thereby inventing the modern digital computer. But we are jumping ahead. Boole, regarded as a gentleman (in fact so courteous and well mannered that he intimidated women who felt "evil" and "inadequate" in front of such a saintly man), married a cranky lady. One day, while in his 40's Boole would catch a minor cold. His wife thought that his cold can be cured by wrapping him in freezing blankets. Boole died of pneumonia.After so many logics, the logic I seek is yet to be discovered
This is integrity !! What russell unearthed, was a curious paradox - the Russell's paradox, which would defy explanation for decades. Martin Davis takes us to visit Cantor and talks about transfinite induction, proving that some infinities are bigger than others ! We visit Hilbert, who once, walked for weeks with torn trousers (his colleagues and students out of politeness, did not point it out, but asked his assistant to gently point it out to Hilbert). When Hilbert's assistant takes Hilbert for a walk near some thorny bushes and says "Probably one of the thorns has torn your trousers", Hilbert famously replied:There is nothing worse that can happen to a scientist than to have his foundation collapse just as the work is finished. I have been placed in this position by Mr Bertrand Russell
"Dont worry, I have been wearing this for weeks and nobody noticed"